TRIGONOMETRY ANGLES OF ELEVATION AND DEPRESSION QUESTIONS

Question 1 :

From the top and foot of a 40 m high tower, the angles of elevation of the top of a lighthouse are found to be 30° and 60° respectively. Find the height of the lighthouse. Also find the distance of the top of the lighthouse from the foot of the tower.

Solution :

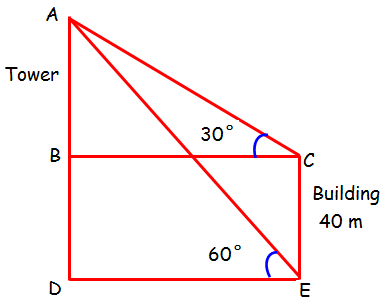
AB = x m and BD = 40 m

In triangle ABC :

∠ACB  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  AB/BC

1/√3  =  x/BC

BC = x√3 ----(1)

In triangle ADE :

∠AED  =  60°

  tan θ = opposite side/Adjacent side

tan 60°  =  AD/DE

√3  =  (x + 40)/DE

DE  =  (x + 40)/√3  ---->(2) 

(1) = (2)

 x√3  =  (x + 40)/√3 

  3 x =  x + 40

3x - x = 40

2x = 40

x = 20

Height of the tower = 40 + 20 = 60 m

Question 2 :

The angle of elevation of a hovering helicopter as seen from a point 45 m above a lake is 30° and the angle of depression of its reflection in the lake, as seen from the same point and at the same time, is 60°. Find the distance of the helicopter from the surface of the lake.

Solution :

From the given information, we can draw a rough diagram 

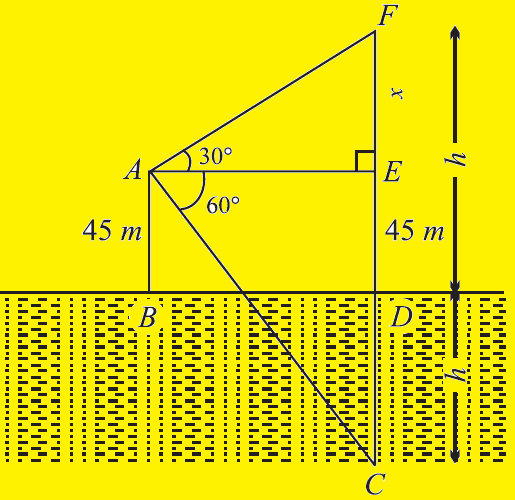
In a right triangle FAE :

  tan θ = opposite side/Adjacent side

tan 30°  =  FE/AE

1/√3  =  (h-45)/AE 

AE = (h - 45) √3 ----(1)

In right triangle ACE :

  tan θ = opposite side/Adjacent side

tan 60°  =  EC/AE

√3  =  (ED+DC)/AE

√3 = (45+h)/AE 

AE  =  (45 + h)/√3----(2)

(1)  =  (2) (BC = AD)

(h - 45) √3 = (45 + h)/√3

3(h - 45) = 45 + h

3h - 135 = 45 + h

2h = 45 + 135

2h  = 180

h = 90

Hence the distance of the helicopter from the surface of the lake is 90 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.