TRIGONOMETRY PROBLEMS WITH SOLUTIONS

Problem 1 :

Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200[(√3  + 1)/√3] metres, find the height of the lighthouse.

Solution :

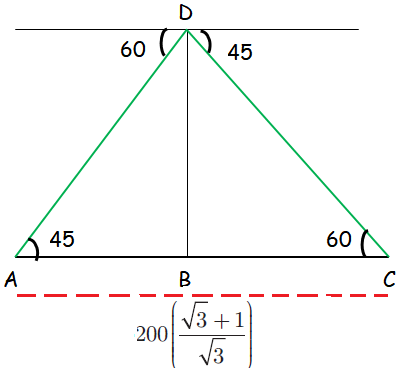
In triangle ABD

tan 45  =  DB/AB

1  =  DB/AB

AB  =  DB  ---------(1)

In triangle DBC,

tan 60  =  DB/BC

√3  =  DB/BC

BC  =  DB/√3  ---------(2)

(1) + (2)

AB + BC  =  200[(√3+1)/√3]

DB + (DB/√3)  =   200[(√3+1)/√3]

DB(1 + (1/√3))  =   200[(√3+1)/√3]

DB[(√3+1)/√3]  =  200[(√3+1)/√3]

DB  =  200

Hence the height of the light house is 200 m.

Problem 2 :

A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34° . Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)

Solution :

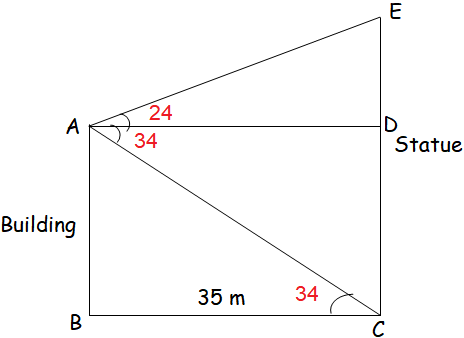
In triangle AED,

tan 24  =  ED/AD

0.4452  =  ED/35

ED  =  0.4452(35)

ED  =  15.582

In triangle ABC, 

tan 34  =  AB/BC

0.6745  =  AB/35

0.6745(35)  =  AB

AB  =  23.60

AB  =  DC

Height of statue  =  15.58 + 23.60 

  =  39.18 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.