TRIGONOMETRY QUESTIONS WORKSHEET FOR GRADE 11

Problem 1 :

Prove that

(i) tan(45° + A)  =  (1 + tanA)/(1 − tanA)

(ii) tan(45° − A) =   (1 + tanA)/(1 − tanA)

Problem 2 :

Prove :

cot(A + B) = (cotAcotB − 1)/(cotA + cotB)

Problem 3 :

If tan x = n/(n + 1) and tan y = 1/(2n + 1) , find tan(x + y).

Solutions

Problem 1 :

Show that

(i) tan(45° + A)  =  (1 + tanA)/(1 − tanA)

(ii) tan(45° − A) =   (1 + tanA)/(1 − tanA)

Solution :

(i) tan(45° + A)  =  (1 + tanA)/(1 − tanA)

tan (A + B)  =  (tan A + tan B) / (1 - tan A tan B)

  =  (tan 45° + tan A) / (1 - tan 45° tan A)

The value of tan 45° is 1.

  =  (1 + tan A) / (1 - tan A)

(ii) tan(45° − A) =   (1 + tanA)/(1 − tanA)

Solution :

tan (A - B)  =  (tan A - tan B) / (1 + tan A tan B)

  =  (tan 45° - tan A) / (1 + tan 45° tan A)

The value of tan 45° is 1.

  =  (1 - tan A) / (1 + tan A)

Problem 2 :

Prove that cot(A + B) = (cotAcotB − 1)/(cotA + cotB)

Solution :

L.H.S 

cot(A + B) =  cos (A + B) / sin (A + B)

  =  (cos A cos B - sin A sin B) / (sin A cos B + cos A sin B)

By dividing every terms by sin A sin B, we get

  =  (cot A cot B - 1) / (cot B + cot A)

  =  (cot A cot B - 1) / (cot A + cot B)  ---> R.H.S

Hence proved.

Problem 3 :

If tan x = n/(n + 1) and tan y = 1/(2n + 1) , find tan(x + y).

Solution :

tan(x + y)  =  (tan x + tan y) / (1 - tanx  tan y)

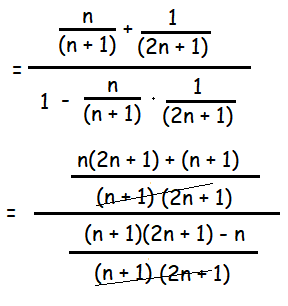
  =  n(2n + 1) + (n + 1) / (n + 1)(2n + 1) - n

  =  (2n² + n + n + 1)  / (2n² + n + 2n + 1 - n)

  =  (2n² + 2n + 1)  / (2n² + 2n + 1)

tan(x + y)  =  1

So, the value of tan(x + y) is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.