TRIGONOMETRY WORKSHEET FOR GRADE 11

(1)  Identify the quadrant in which an angle of each given measure lies

(i) 25^◦ (ii) 825^◦ (iii) −55^◦ (iv) 328^◦ (v) −230^◦  

Solution

(2)  For each given angle, find a coterminal angle with measure of θ such that 0^◦ ≤ θ < 360^◦

(i) 395^◦ (ii) 525^◦ (iii) 1150^◦ (iv) −270^◦ (v) −450^◦

Solution

(3)  If a cos θ − b sin θ = c, show that a sin θ + b cos θ = ± √a² + b² − c².      Solution

(4)  If sin θ + cos θ = m, show that cos⁶ θ + sin⁶ θ = 4 − 3 (m² − 1)²/4, where m² ≤ 2.         Solution

(5)  If (cos⁴ α/cos² β) + (sin⁴ α/sin² β)  =  1, prove that

(i)  sin⁴ α + sin⁴ β = 2sin² α sin² β

(ii) (cos⁴ β/cos² α) + (sin⁴ β/sin² α)  =  1.    Solution

(6)  If y = 2 sinα/(1 + cos α + sinα), then prove that (1 − cos α + sinα)/(1 + sinα) = y.               Solution

(7)   

Solution

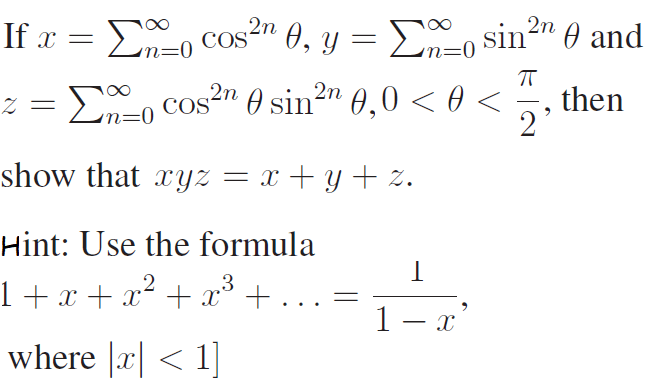
(8)  If tan² θ = 1 − k², show that sec θ + tan³ θ cosec θ = (2−k²)^3/2. Also, find the values of k for which this result holds.      Solution

(9)  If sec θ + tanθ = p, obtain the values of sec θ, tan θ and sin θ in terms of p    Solution

(10)  If cot θ (1 + sin θ) = 4m and cot θ (1 − sin θ) = 4n, then prove that (m² − n²)² = mn     Solution

(11)  If cosec θ − sin θ = a³ and sec θ − cos θ = b³, then prove that a²b² (a² + b²)  =  1.         Solution

(12)  Eliminate θ from the equations a sec θ − c tan θ = b and bsec θ + d tan θ = c.     Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.