TWO POINT FORM EQUATION OF A LINE

Let A(x₁, y₁) and B(x₂, y₂) be two given distinct points on a line as shown below.

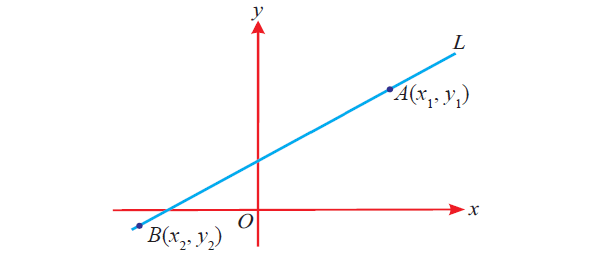
Slope of the straight line passing through these points is given by

Point-Slope form equation of a line, 

y - y₁ = m(x - x₁)

The above is the equation of a line in two-point form.

Example 1 :

Find the general equation of a line passing through the points (-2, 1) and (4, -7).

Solution :

Given : Two points on the straight line : (-2, 1) and (4, -7).

Equation of line in two-point form :

y - y₁ = [(y₂ - y₁)/(x₂ - x₁)](x - x₁)

Substitute (x₁ , y₁) = (-2, 1) and (x₂, y₂) = (4, -7).

y - 1 = [(-7 - 1)/(4 + 2)](x + 2)

y - 1 = (-8/6)(x + 2)

y - 1 = -(4/3)(x + 2)

3(y - 1) = -4(x + 2)

3y - 3 = -4x - 8

4x + 3y + 5 = 0

Example 2 :

Find the equation of a line in slope-intercept form which passing through the points (-2, 5) and (3, 6).

Solution :

Given : Two points on the straight line : (-2, 5) and (3, 6).

Equation of line in two-point form :

y - y₁ = [(y₂ - y₁)/(x₂ - x₁)](x - x₁)

Substitute (x₁ , y₁) = (-2, 5) and (x₂, y₂) = (3, 6).

y - 5 = [(6 - 5)/(3 + 2)](x + 2)

y - 5 = (1/5)(x + 2)

y - 5 = (1/5)x + 2/5

y = (1/5)x + 2/5 + 5

y = (1/5)x + 27/5

Example 3 :

The vertices of a triangle ABC are A(2, 1), B(-2, 3) and C(4, 5). Find the equation of the median through the vertex A.

Solution :

Median is a straight line joining a vertex and the midpoint of the opposite side.

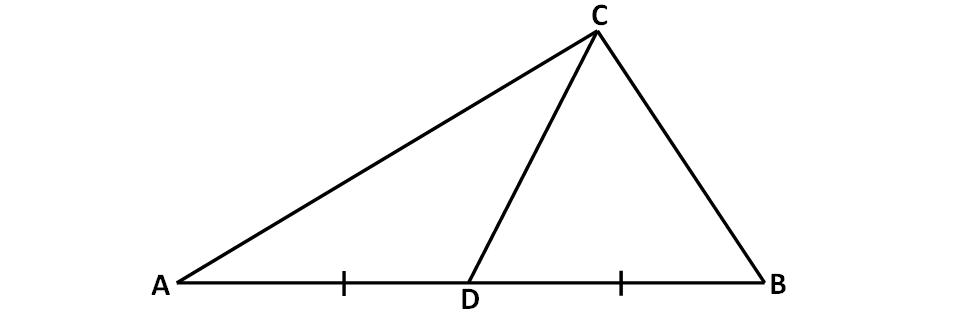
In ΔABC above, midpoint of BC :

= D((-2 + 4)/2, (3 + 5)/2)

= D(1, 4)

The median through A is the line joining two points A (2, 1) and D(1, 4).

Equation of the median through A :

y - y₁ = [(y₂ - y₁)/(x₂ - x₁)](x - x₁)

Substitute (x₁ , y₁) = (2, 1) and (x₂, y₂) = (1, 4).

y - 1 = [(4 - 1)/(1 - 2)](x - 2)

y - 1 = (3/-1)(x - 2)

y - 1 = -3(x - 2)

y - 1 = -3x + 6

3x + y - 7 = 0

Example 4 :

Two buildings of different heights are located at opposite sides of each other. If a heavy rod is attached joining the terrace of the buildings from (6, 10) to (14, 12), find the equation of the rod joining the buildings ?

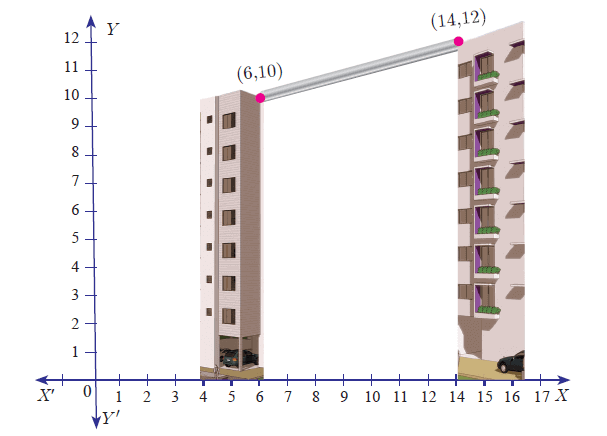
Solution :

The equation of the rod is the equation of the line passing through the two points (6, 10) and (14, 12).

Equation of the line in two-point form :

y - y₁ = [(y₂ - y₁)/(x₂ - x₁)](x - x₁)

Substitute (x₁ , y₁) = (6, 10) and (x₂, y₂) = (14, 12).

y - 10 = [(12 - 10)/(14 - 6)](x -6)

y - 10 = (2/8)(x - 6)

y - 10 = (1/4)(x - 6)

4(y - 10) = x - 6

4y - 40 = x - 6

x - 4y + 34 = 0

Hence, equation of the rod is x - 4y + 34 = 0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.