UNION AND INTERSECTION PRACTICE PROBLEMS

Question 1 :

Place the elements of the following sets in the proper location on the given Venn diagram.

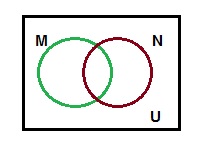
U  =  {5, 6, 7, 8, 9, 10, 11, 12, 13}

M  =  {5, 8, 10, 11}

N  =   {5, 6, 7, 9, 10}.

Solution :

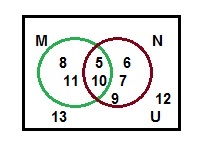
Question 2 :

If A and B are two sets such that A has 50 elements, B has 65 elements and A∪B has 100 elements, how many elements in A∩B?

Solution :

Given n(A)  =  50, n(B)  =  65, n(A∪B)  =  100

By the rule,

n(A∪B)  =  n(A) + n(B) - n(A∩B)

n(A∩B)  =  n(A) + n(B) - n(A∪B)

=  50+65-100

=  115-100

=  15

Question 3 :

If A and B are two sets containing 13 and 16 elements respectively, then find the minimum and maximum number of elements in A∪B?

Solution :

n(A)  =  13 and n(B)  =  16

n( A∪B) must be either the elements of the bigger set, that is B or the addition of number of elements in both A and B.

If A is the subset of B, then  A∪B is the set B itself. Then the number of A∪B is number of B itself. That is the minimum number of  A∪B.

So minimum of  A∪B is 16.

If A and B are two disjoint sets, then number of elements in  A∪B is the total number of elements in both A and B. 

So, the maximum of A∪B is 13+16  =  29.

Question 4 :

If n( A∩B)  =  5, n(A∪B)  =  35, n(A)  =  13, find n(B)?

Solution :

By the rule

n(A∪B) = n(A) + n(B) - n(A∩B)

n(B) = n(A∪B)+n(A∩B)-n(A)

=  35 + 5 - 13

n(B) = 27

Question 5 :

If n(A) = 26, n(B) = 10, n(A∪B) = 30, n(A') =17, find n(A∩B) and n(U)?

Solution :

n(A∪B)  =  n(A)+n(B)-n(A∩B)

n(A∩B)  =  n(A)+n(B)-n(A∪B)

n(A∩B)  =  26+10-30

n(A∩B)  =  6

n(A) + n(A')  =  n(U)

n(U)  =  26+17

n(U)  =  43

Question 6 :

If n(U) = 38, n(A) = 16,  n(A∩B) = 12, n(B') = 20, find n(A∪B)?

Solution :

n(A) + n(A') =  n(U)

n(B)  =  n(U)-n(B')

n(B)  =  38 - 20

n(B)  =  18

n(A∪B) =  n(A)+n(B)- n(A∩B)

n(A∪B)  =  16+18-12

n(A∪B)  =  34-12

n(A∪B)  =  22

Question 7 :

Let A and B be two finite sets such that n(A-B) = 30, n(A∪B) = 180, n(A∩B) = 60, find n(B)?

Solution :

n(A)  =  n(A-B) + n(AnB)

n(A)  =  30+60

n(A)  =  90

n(AuB)  =  n(A) + n(B) - n(AnB)

180  =  90 + n(B) - 60

180-30  =  n(B)

n(B)  =  150

Question 8 :

Of 50 cat and dog owners surveyed, 25 have a cat. Ten owners have a dog and a cat. How many owners have a dog?

Solution :

Let A and B be the people who are having cat and dog.

Number of people have cat and dog = n (AUB) = 50

Number of people having cat n(A) = 25

Number of people having dog n(B) = ?

Number of people who are having cat and dog

n(A n B) = 10

n(AUB) = n(A) + n(B) - n(A n B)

50 = 25 + n(B) - 10

50 = 15 + n(B)

50 - 15 = n(B)

n(B) = 35

Question 9 :

Of 240 college freshmen, 152 are taking history and 81 are taking science and history. How many freshmen are taking history but not science?

Solution :

Let A and B be the people who are taking history and science.

Number of people are taking history and science

n (AUB) = 240

Number of people who are taking history n(A) = 152

Number of people who are taking history and science

n(AnB) = 81

Number of people who are taking history but not science 

= n(A) - n(AnB)

= 152 - 81

= 71

Question 10 :

Find two sets A and B such that

A U B = {1,2,3,4,5} and AnB = {2}.

Solution :

The set A may consist of elements including 2.

A = {1, 2}

The set B may consist of elements including 2.

B = {2, 3, 4, 5}

Question 11 :

Let M = {x | x is a multiple of 3} and N = {x | x is a multiple of 4}. Describe the intersection of M and N.

Solution :

Given that,

M = {x | x is a multiple of 3}

N = {x | x is a multiple of 4}

M = {3, 6, 9, 12, 15, 18, ...............}

N = {4, 8, 12, 16, 20, ..................}

To find the intersection of M and N, we should find the multiples of 12.

MnN = {12, 16, 20, 24, .............}

Question 12 :

Set X has 10 elements, set Y has 15 elements, and X n Y has 5 elements. How many elements are in X U Y?

Solution :

Number of elements in set X, n(X) = 10

Number of elements in set Y, n(Y) = 15

n(XnY) = 5

n(XUY) = n(X) + n(Y) - n(XnY)

= 10 + 15 - 5

= 25 - 5

n(XUY) = 20

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.