USE MODELS TO FIND AREAS OF COMPOSITE SHAPES

Example 1 : 

Find the area of the shaded region.

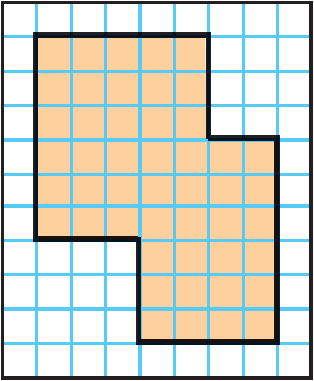
Solution :

One way : 

Count the square units. The shape shows that there are 48 square units.

Another Way :

Step 1 :

Decompose the shape into rectangles and squares.

The shape can be broken into two rectangles and one square as given below.

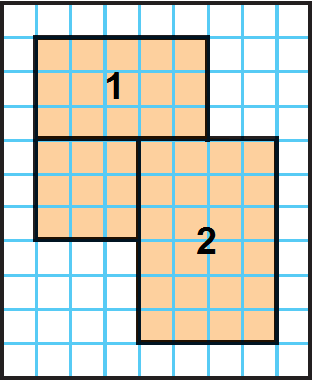
Step 2 :

Find the area of the parts. Then add them together.

Area of rectangle 1 :  3 × 5 = 15

Area of square  :  3 × 3 = 9

Area of rectangle 2 :  4 × 6 = 24

Area of the given composite shape is

=  15 + 24 + 9 

=  48 square units

Example 2 : 

Find the area of the shaded region.

Solution :

Step 1 :

Decompose the shape into parts.

The shape can be broken into one rectangle and one square as given below. 

Step 2 :

Find the area of the parts. Then add them together.

Area of rectangle  :  2 × 4 = 8

Area of square  :  3 × 3 = 9

Area of the given composite shape is

=  8 + 9 

=  17 square units

Example 3 : 

Find the area of the shaded region.

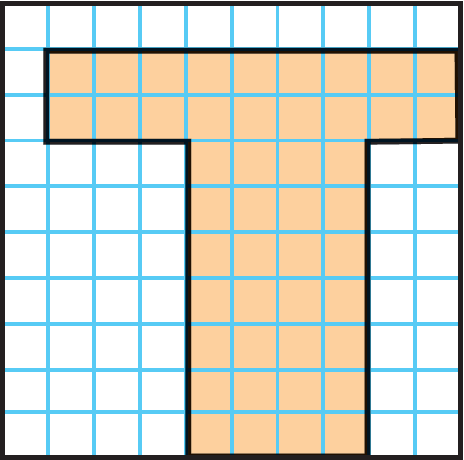
Solution :

Step 1 :

Decompose the shape into parts.

The shape can be broken into two rectangles as given below. 

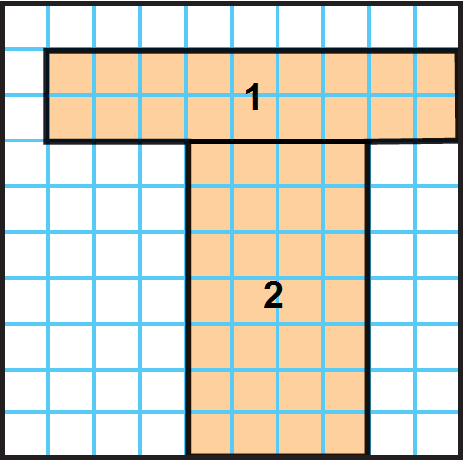
Step 2 :

Find the area of the parts. Then add them together.

Area of rectangle 1  :  9 × 2 = 18 

Area of rectangle 2  :  4 × 7 = 28

Area of the given composite shape is

=  18 + 28 

=  46 square units

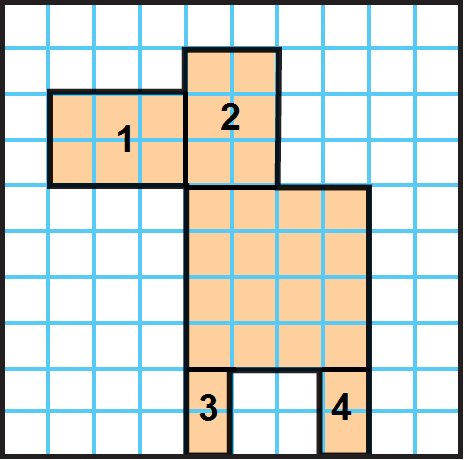
Example 4 : 

Find the area of the shaded region.

Solution :

Step 1 :

Decompose the shape into parts.

The shape can be broken into four rectangles and one square as given below. 

Step 2 :

Find the area of the parts. Then add them together.

Area of rectangle 1  :  3 × 2 = 6 

Area of rectangle 2  :  2 × 3 = 6

Area of square  :  4 × 4 = 16

Area of rectangle 3  :  1 × 2 = 2

Area of rectangle 4  :  1 × 2 = 2

Area of the given composite shape is

=  6 + 6 + 16 + 2 + 2 

=  32 square units

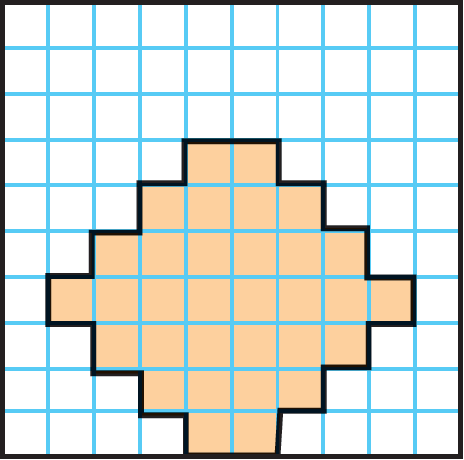
Example 5 : 

Find the area of the shaded region.

Solution :

Count the square units inside the shaded region. The shape shows that there are 32 square units.

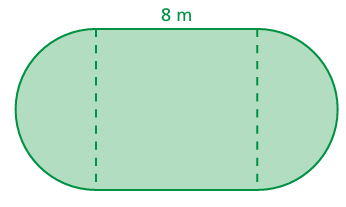
Example 6 : 

The figure is made up of a square and two semicircles. Find the perimeter.

Solution :

In the given figure, we see the square portion in the middle and two semi circular shapes.

Side length of square = 8 m and diameter of the semicircular = 8 m and radius = 4 m.

Perimeter of the figure

= 2(side length of square) + 2(perimeter of semi circle)

= 2(a²) + 2(1/2)  (πr)

= 2(8²) + 3.14 x 4

= 2(64) + 12.56

= 128 + 12.56

= 140.56 meter

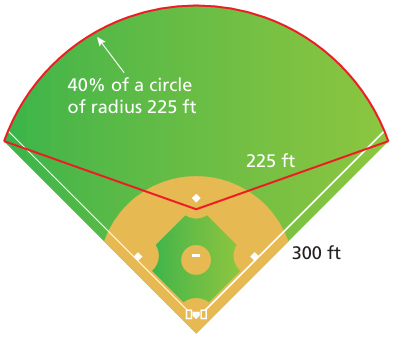
Example 7 : 

Running at 4 ft/sec, how long would it take a person to run around the baseball field?

Solution :

Perimeter of shape = 40% of circumference of semicircle + 2(radius) + 2(300)

= 40% of πr + 2(225) + 2(300)

= 0.40 x 3.14 x 225 + 2(225) + 2(300)

= 282.6 + 450 + 600

= 1332.6 ft

Time = distance / speed

= 1332.6/4

= 333.15 seconds

1 minute = 60 seconds

= 333.15/60

= 5.55 minutes

= 5 + 0.55(60 seconds)

= 5 minutes 33 seconds

Example 8 : 

A garden is built on a rooftop. Find the perimeter of the garden.

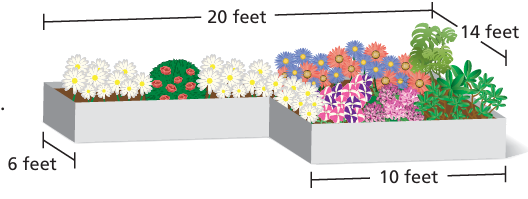
Solution :

Perimeter of the shape = 20 + 14 + 10 + 6 + 10 + 6

= 66 feet

Example 9 : 

Dimensions of a painting are 60 cm × 38 cm. Find the area of the wooden frame of width 6 cm around the painting as shown

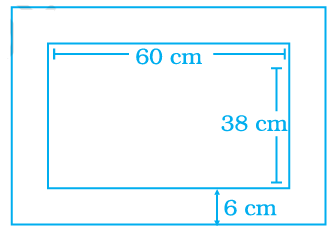
Solution :

Area of wooden frame = area of larger rectangle outside - area of rectangle inside

Dimension of rectangle outside :

Length = 60 + 6 + 6 ==> 72 cm

Width = 38 + 6 + 6 ==> 50 cm

Dimension of rectangle inside :

Length = 60 cm

Width = 38 cm

Area of the frame = 72 x 50 - 60 x 38

= 3600 - 2280

= 720 cm²

Example 10 : 

A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.

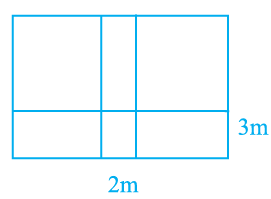
Solution :

Length of playground = 120 m

Width = 80 m

Area of path with width of 2 m :

= (80 - 3) x (120 - 2)

= 77 x 118

= 9086 square meter

So, area of the play ground is 9086 square meter.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.