USING CONVERSION FACTORS TO SOLVE PROBLEMS

We solve many real word problems by converting units within measurement system (metric or customary)  and between measurement systems (customary to metric or metric to customary). 

We use conversion factors to convert units within measurement system and between measurement systems. 

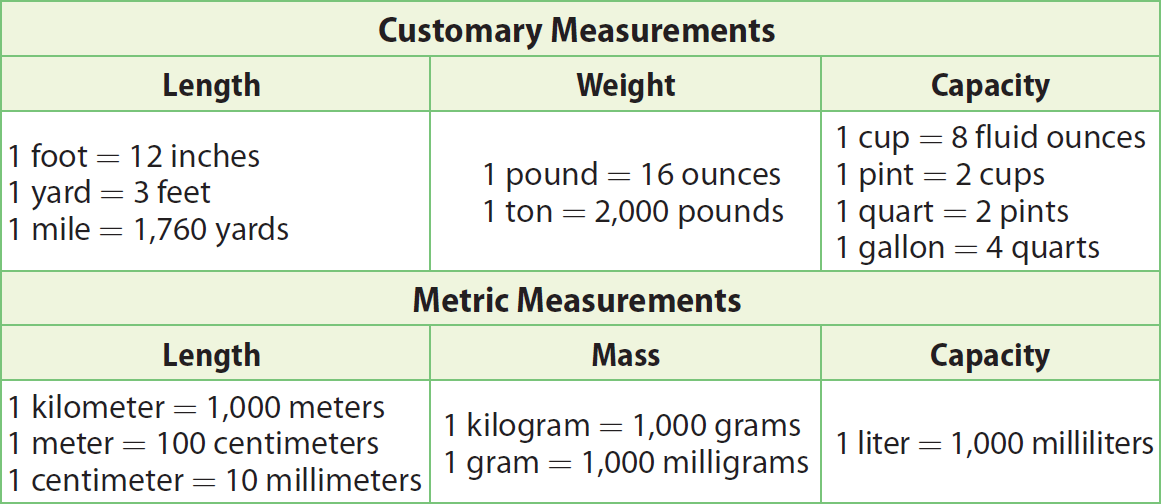
The chart given below can be used to convert units within measurement system. 

The chart given below can be used to convert units between measurement systems. 

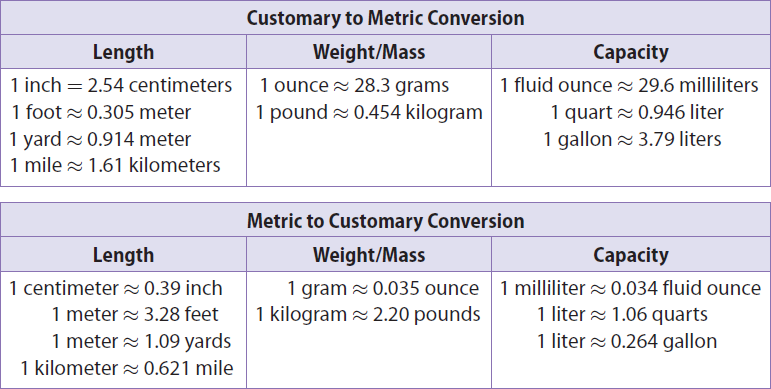
For example, 

From the above chart, in the length section of customary to metric conversion, we have

 1 inch   =  2.54 centimeters

If we convert inches into cm, the conversion factor is 

2.54 cm / 1 inch

If we convert cm into inches, the conversion factor is 

1 inch  / 2.54

Example 1 :

Elena wants to buy 2 gallons of milk but can only find quart containers for sale. How many quarts does she need ?

Solution :

Step 1 :

We want to convert gallons to quarts.

Identify the ratio that compares the units involved.

The units gallons and quarts are customary units of capacity.

Find the relationship of those units in the capacity section of the customary measurements table.

4 quarts  =  1 gallon

The appropriate conversion factor is 4/1.

Because when we multiply 2 gallons by that conversion factor, we can divide out the common unit gallons. The resulting unit is quarts.

Step 2 :

Multiply the given measurement by the conversion factor.

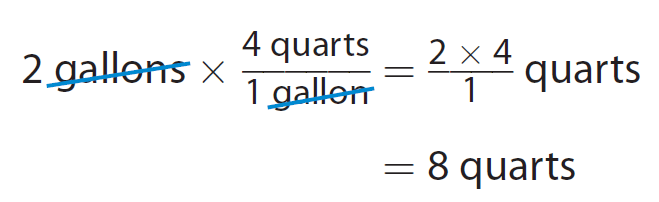
Elena needs 8 quarts of milk.

Example 2 :

A container of a powdered fruit drink mix has a mass of 1.25 kilograms. What is that mass in milligrams ?

Solution :

Step 1 :

You want to convert kilograms to milligrams.

There is no equation in the table that relates kilograms and milligrams directly. However, we can convert kilograms to grams first. Then we can convert grams to milligrams.

Step 2 :

Multiply the given measurement by the conversion factor.

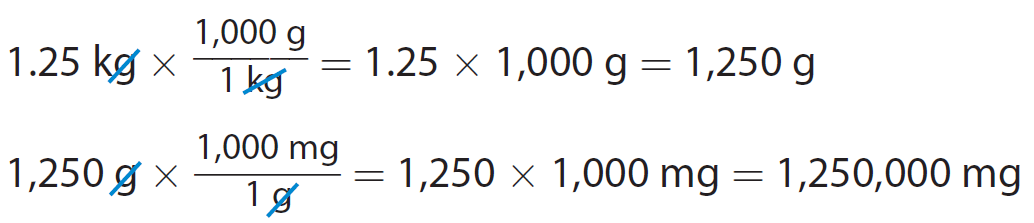
We can also do both conversions at the same time.

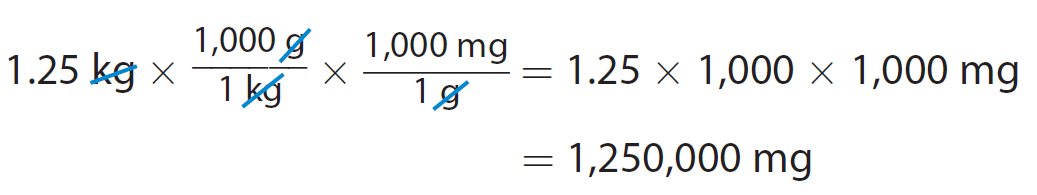
A mass of 1.25 kilograms is equal to 1,250,000 milligrams.

Example 3 :

While working out, Alima adds 11.35 kilograms to the machine. About how many pounds does she add ?

Solution :

Step 1 :

Find the conversion factor for converting kilograms to pounds

1 kilogram ≃  2.20 pounds

Write the conversion factor as a ratio

2.20 pounds / 1 kilogram

Step 2 :

Convert the given measurement.

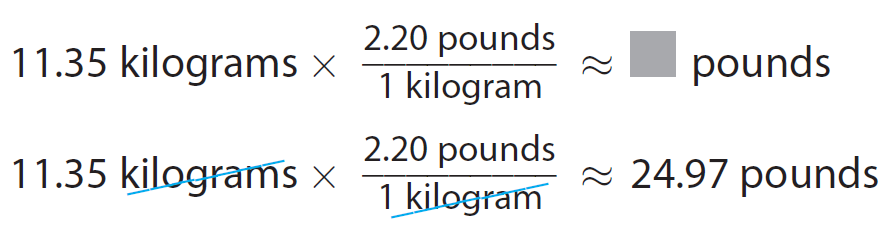
Alima adds about 25 pounds.

Example 4 :

Bob’s driveway is 45 feet long by 18 feet wide. He plans to pave the entire driveway. The asphalt paving costs $24 per square meter. What will be the total cost of the paving ?

Solution :

Step 1 :

First find the dimensions of the driveway in meters.

Convert each measurement to meters.

Use 1 foot ≃ 0.305 meter.

Step 2 :

Next find the area in square meters.

Area  =  length × width

≃  13.725 × 5.49

≃  75.35025 square meters

Step 3 :

Now find the total cost of the paving.

square meters × cost per square meter = total cost

75.35025 × $24  ≃  $1,808.41

Total cost of paving is $1808.41.

Example 5 :

Peter is overweight. He is 105 kg. His aim is to lose 500 g per week. If he manages this, how many weeks will it be until he is 90 kg?

Solution :

Peter's weight = 105 kg

Each week he is trying to reduce = 500 grams

Number of weeks is taken to have the weight of 90 kg = n

Converting grams to kg

1 kg = 1000 grams

dividing by 2, we get

1/2 kg = 500 grams

0.5 kg = 500 grams

105 - 0.5n = 90

Adding 0.5 n on both sides

105 = 90 + 0.5 n

Subtracting 90 on both sides

105-90 = 0.5n

15 = 0.5n

Dividing by 0.5 on both sides

15/0.5 = n

30 = n

So, it takes 30 weeks to have the weight of 90 kg.

Example 6 :

30 g serving of a certain breakfast cereal has 0.5 g of salt. How much salt would that be in milligrams

Solution :

1 gram = 10 milligrams

30 g serving will have 0.5 gram of salt

Converting grams to mg

30 grams = 300 milligrams

From the information,

30 grams of serving = 0.5 grams of salt

300 grams of serving = 10 x 0.5

= 5 grams of salt

Using the conversion above, 

5 grams = 5(10)

= 50 milligrams

Example 7 :

Chase measured a line for his art project. It is 200 millimeters long. How many centimeters is the line?

Solution :

1 cm = 10 mm ----(1)

200 mm = ? cm

Multiply by 20 on both sides

20 cm = 200 mm

So, the length of the line is 20 cm.

Example 8 :

Cheryl is moving to a new house. Her old house is 3 kilometers from her new house. How many meters is the old house from the new house?

Solution :

1 km = 1000 meters

3 km = 3(1000)

= 3000 meters

So, the distance between the old house and new house is 3000 meters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.