USING MEAN METHOD TO FIND RATIONAL NUMBERS BETWEEN TWO NUMBERS

Question 1 :

Using average, write 3 rational numbers between (14/5) and (16/3)

Solution :

Let a  =  14/5, b = 16/3

Let c, d, e be the 3 rational numbers between the given numbers.

c  =  (a + b)/2

c  =  [(14/5) + (16/3)]/2  

L.C.M (5, 3)  =  15

c  =  (42 + 80)/30

c  =  122/30

c  =  61/15

d  =  (a + c)/2

d  =  [(14/5) + (61/15)]/2  

d  =  (42 + 61)/30

d  =  103/30

e  =  (a + d)/2

e  =  [(14/5) + (103/30)]/2  

e  =  (84 + 103)/60

e  =  187/60

So, the three rational numbers between the given numbers are 61/15, 103/30 and 187/60

Question 2 :

Verify that −(−x) is the same x for:

(i)  x  =  11/15

Solution :

-(-x)  =  - (-11/15)   =  11/15

(ii)  x  =  -31/45

Solution :

x  =  -31/45

-x  =  -(-31/45)

-x  =  31/45

-(-x)  =  -31/45

Hence proved.

Question 3 :

Re-arrange suitably and add :

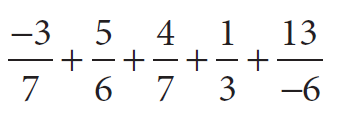
Solution :

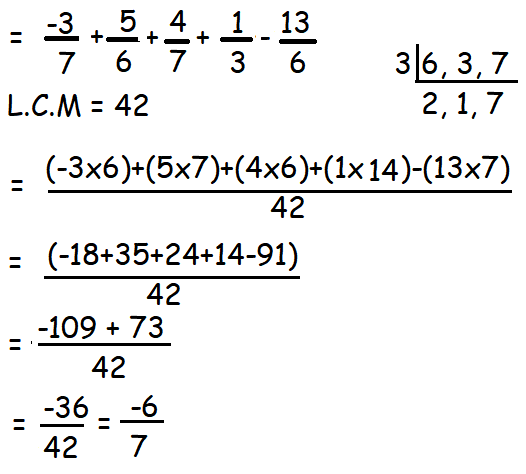
Mixed Questions on Adding Subtracting Multiplying and Dividing Fractions

Question 4 :

What should be added to -8/9 to get 2/5 ?

Solution :

Let "x" be the required rational number to be added.

(-8/9) + x  =  2/5

x  =  (2/5) + (8/9)

L.C.M (5, 9)  =  45

x  =  [2(9) + 5(8)]/45

x  =  [18 + 40]/45

x  =  58/45

Question 5 :

Subtract -8/44 from -17/11

Solution :

  =  (-17/11) - (-8/44)

  =  (-17/11) + (8/44)

  =  [-17(4) + 8]/44

  =  [-68 + 8]/44

  =  -60/44

  =  -15/11

Question 6 :

Evaluate: (i)  (9/2) x (-11/3)

Solution :

  =  (9/2) x (-11/3)

  =  (3/2) x (-11)

  =  -33/2

(ii)  (-7/27) x (24/(-35))

Solution :

  =  (-7/27) x (24/(-35))

By canceling 7 and 35, we get 5. In the same way by canceling 27 and 24, we get 8/9

  =  (-1/9) x (-8/5)

  =  8/45

Question 7 :

Divide (i) (-21/5) by (-7/-10)

Solution :

  =   (-21/5) by (-7/-10)

  =   (-21/5) x (10/7)

  =  -3 x 2

  =  -6

(ii) (-3/13) by (-3)

Solution :

  =   (-3/13) by (-3)

  =   (-3/13) x (-1/3)

  =  1/13

(iii) -2 by -6/15

Solution :

  =   (-2) by (-6/15)

  =   (-2) x (-15/6)

  =  5

Question 8 :

Simplify (2/5 + 3/2) ÷ (3/10) as a rational number and show that it is between 6 and 7.

Solution :

  =  (2/5 + 3/2) ÷ (3/10)

  =  [(4+15)/10] ÷ (3/10)

  =  (19/10) x (10/3)

  =  19/3

=  6  1/3

Hence the rational numbers lies between 6 and 7.

Question 9 :

Write five rational numbers which are less than –2.

Solution :

All integers are rational numbers. So the integers -7, -6, -5, -4, -3 are rational numbers less than -2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.