USING MULTIPLICATION TO SOLVE EQUATIONS

Example 1 :

Solve the following equation and graph the solution on a number line.

x/5 = 10

Solution :

Since we are trying to solve for x, we have to get rid of 5 which divides x in the above equation.

To get rid of 5, we have to multiply both sides of the equation by 5.

(x/5) x 5 = 10 x 5

x = 50

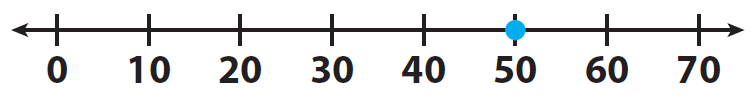
Example 2 :

Solve the equation and and graph the solution on a number line.

15 = r/2

Solution :

15 = r/2

Multiply both sides by 2.

15 x 2 = (r/2) x 2

30 = r

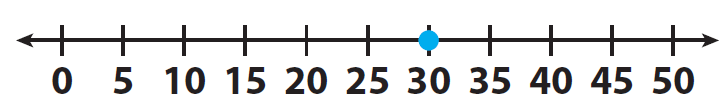
Example 3 :

Solve the equation and graph the solution on a number line.

y/9 = 1

Solution :

y/9 = 1

Multiply both sides by 9.

(y/9) x 9 = 1 x 9

y = 9

Example 4 :

John had some candies. He shared the candies equally to his 3 kids. If each kid had received 7 candies, how many candies did John have ?

Solution :

Let m be the number of candies that John had initially.

m/3 = 7

Multiply both sides by 3 to solve for m.

(m/3) x 3 = 7 x 3

m = 21

Hence, John initially had 21 candies.

Example 5 :

The speed of John is 50 miles per hour. If he covers one-fifth of a certain distance in 2 hours, find the actual distance.

Solution :

Let d be the actual distance.

distance = speed x time

(1/5)d = 50 x 2

d/5 = 100

Multiply both sides by 5.

(d/5) x 5 = 100 x 5

d = 500

The actual distance is 500 miles.

Example 6 :

Ronald is x years old. His friend Colin is 3 years older than than Ronald. Colin is 19 years old.

(a) Write down an equation for this information.

(b) Solve your equation to find how old Ronald is.

Solution :

Age of Ronald = x

Age of Colin = x + 3

Age of Colin = 19 years

x + 3 = 19

x = 19 - 3

x = 16

Age of Ronald is 16 years old.

Example 7 :

Hannah is n years old. Her aunt Emily is three times older than Hannah. Emily is 48 years old.

(a) Write down an equation for this information.

(b) Solve your equation to ind how old Hannah is 

Solution :

a) Age of Hannah = n

Emily's age = 3n

The required equation is,

n + 3n = 48

b) 4n = 48

n = 48/4

n = 12

So, age of Hannah is 12 years old.

Example 8 :

Sam thinks of a number, n. He multiplies his number by 7 and then adds 3 to the result. His final answer is 45.

(a) Write down an equation for this information.

(b) Solve your equation to find the number, n.

Solution :

The number Sam thinks is n

Multiplies by 7 and adds by 3 = 45

a) So, the required equation is

7n + 3 = 45

b)  7n = 45 - 3

7n = 42

n = 42/7

n = 6

So, age of Sam is 6 years old.

Example 9 :

A rectangular field has a perimeter of 150 m. The field is 15 metres longer than it is wide. The width of the field is x metres.

(a) Write down an equation for this information.

(b) Solve your equation to ind the width of the field

(c) Find the length of the field.

Solution :

Length of rectangular field = 15

Width of rectangular field = w

Perimeter = 150 m

a)

2(15 + w) = 150

b) Solving the equation :

15 + w = 150/2

15 + w = 75

w = 75 - 15

w = 60 m

c) Finding length :

Lenght = 15 + w

= 15 + 60

= 75 m

Example 10 :

Shown is a triangle. The three angles add up to give 180°

(a) Write down an equation for this information

(b) Solve your equation to find x.

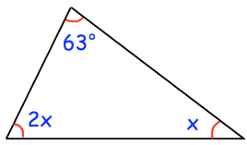
Solution :

a) Creating equation :

Sum of interior angles of triangle = 180

b) Solving the equation :

63 + 2x + x = 180

63 + 3x = 180

3x = 180 - 63

3x = 117

x = 117/3

x = 39

Example 11 :

The sum of each row is given. Find a, b, c a

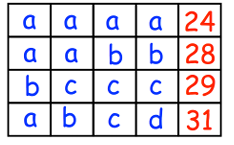
Solution :

By observing the table above 

From the first row :

a + a + a + a = 24

4a = 24

a = 24/4

a = 6

From the second row :

a + a + b + b = 28

2a + 2b = 28

Applying the value of a, we get

2(6) + 2b = 28

12 + 2b = 28

2b = 28 - 12

2b = 16

b = 16/2

b = 8

From the third row :

b + c + c + c = 29

b + 3c = 29

Applying the value of b, we get

8 + 3c = 29

3c = 29 - 8

3c = 21

c = 21/3

c = 7

From the fourth row :

a + b + c + d = 31

Applying the values of a, b and c, we get

6 + 8 + 7 + d = 31

21 + d = 31

d = 31 - 21

d = 10

So, the values of a, b, c and d are 6, 8, 7 and 10 respectively.

Example 12 :

The numerator of a fraction is 2 less than the denominator. If one is added to its denominator, it becomes 1/2 find the fraction.

Solution :

Let x be the denominator.

Numerator = x - 2

(x - 2)/(x + 1) = 1/2

2(x - 2) = 1(x + 1)

2x - 4 = x + 1

2x - x = 1 + 4

x = 5

Numerator = x - 2

= 5 - 2

= 3

So, the fraction is 3/5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.