USING PATTERNS OF INTEGER EXPONENTS

In this section, we are going to see, how to use the patterns of integer exponents to find the forth coming terms in the sequence of numbers. 

 The table below shows powers of 5, 4, and 3.

Question 1 : 

What pattern do you see in the powers of 5 ?

Answer :

As the exponent decreases by 1, the value of the power is divided by 5.

Question 2 : 

What pattern do you see in the powers of 4 ?

Answer :

As the exponent decreases by 1, the value of the power is divided by 4.

Question 3 : 

What pattern do you see in the powers of 3 ?

Answer :

As the exponent decreases by 1, the value of the power is divided by 3.

Question 4 : 

What are the values of 5⁰,  5^-1,  5^-2 and 5^-3 ?

Answer :

From the table, we come to know the fact, as the exponent decreases by 1, the value of the power is divided by 5. 

And also, from the table, we have 5¹ =  5.

Since 5¹  =  5, we get 5⁰  =  5 ÷ 5  =  1.

Since 5⁰ =  1, we get 5^-1  =  1 ÷ 5  =  1/5.

Since 5^-1  =  1/5, we get  5^-2 =  (1/5) ÷ 5  =  1/25.

Since  5^-2  =  1/25, we get 5^-3  =  (1/25) ÷ 5  =  1/125. 

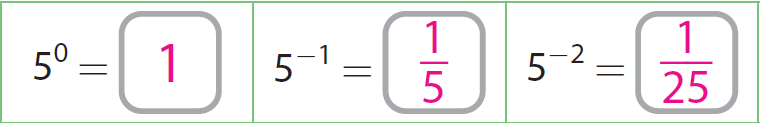
Question 5 : 

What are the values of 4⁰,  4^-1,  4^-2 and 4^-3 ?

Answer :

From the table, we come to know the fact, as the exponent decreases by 1, the value of the power is divided by 4. 

And also, from the table, we have 4¹ =  5.

Since 4¹  =  4, we get 4⁰  =  4 ÷ 4  =  1.

Since 4⁰ =  1, we get 4^-1  =  1 ÷ 4  =  1/4.

Since 4^-1  =  1/4, we get 4^-2  =  (1/4) ÷ 4  =  1/16.

Since  4^-2  =  1/16, we get 4^-3  =  (1/16) ÷ 4  =  1/64.

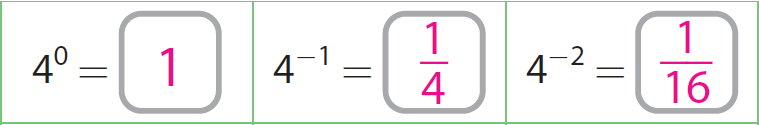
Question 6 : 

What are the values of 3⁰,  3^-1,  3⁻² and 3⁻³ ?

Answer :

From the table, we come to know the fact, as the exponent decreases by 1, the value of the power is divided by 3. 

And also, from the table, we have 3¹  =  3.

Since 3¹  =  3, we get 3⁰  =  3 ÷ 3  =  1.

Since 3⁰  =  1, we get 3^-1  =  1 ÷ 3  =  1/3.

Since 3^-1  =  1/3, we get  3^-2  =  (1/3) ÷ 3  =  1/9.

Since  3^-2  =  1/9, we get 3^-3  =  (1/9) ÷ 3  =  1/27.

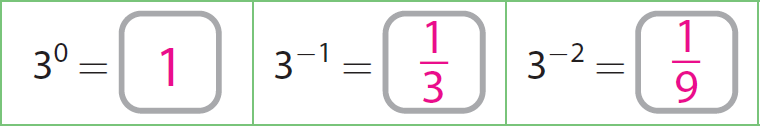
Reflect

1.  Write a general rule for the value of a⁰, a ≠ 0 ?

a⁰  =  1

2.  Write a general rule for the value of a^-n, where a ≠ 0 and n is an integer ?

a^-n  =  1/aⁿ

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.