USING PYTHAGOREAN THEOREM WORKSHEET

Problem 1 :

In the right triangle given below, find the length of the missing side using Pythagorean theorem. 

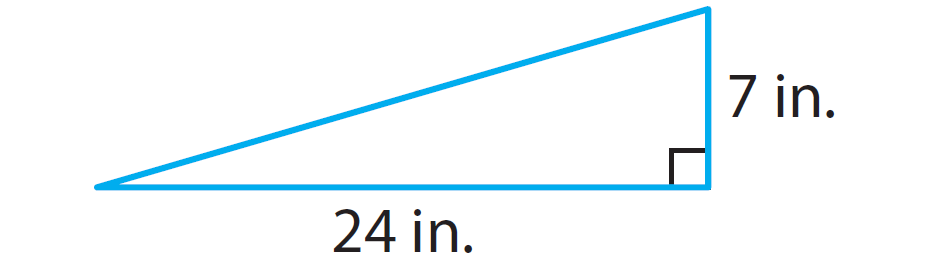
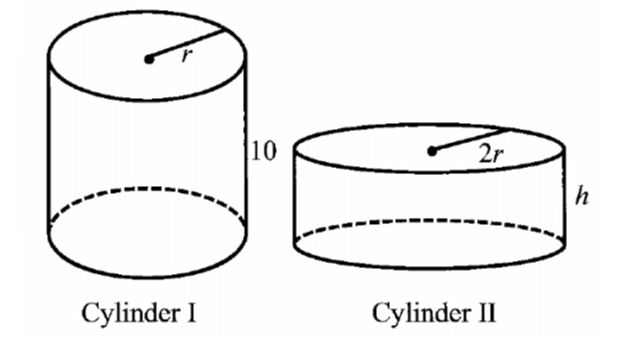
Problem 2 :

In the right triangle given below, find the length of the missing side using Pythagorean theorem. 

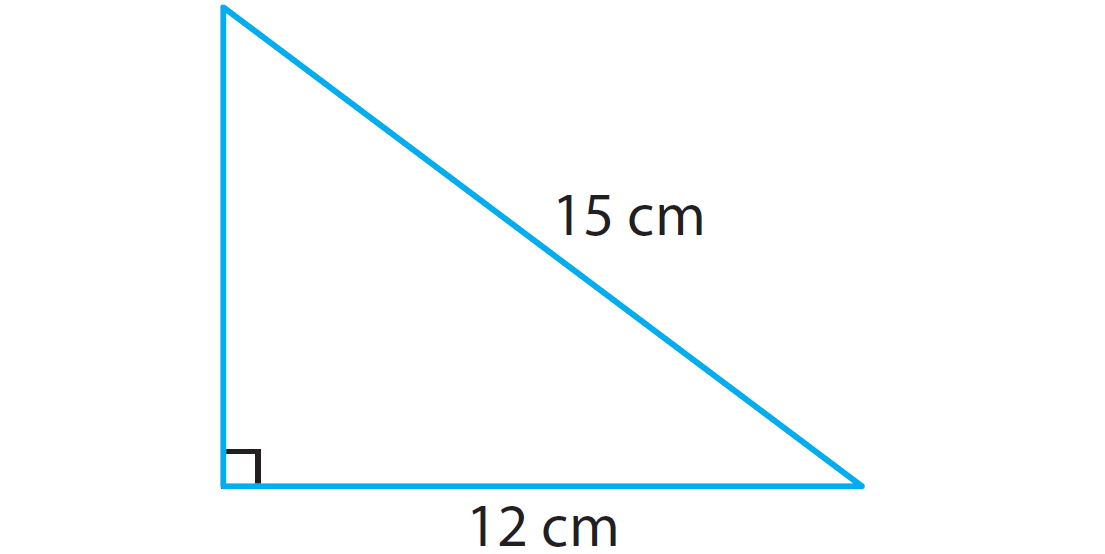
Problem 3 :

In the right triangle given below, find the length of the missing side using Pythagorean theorem. 

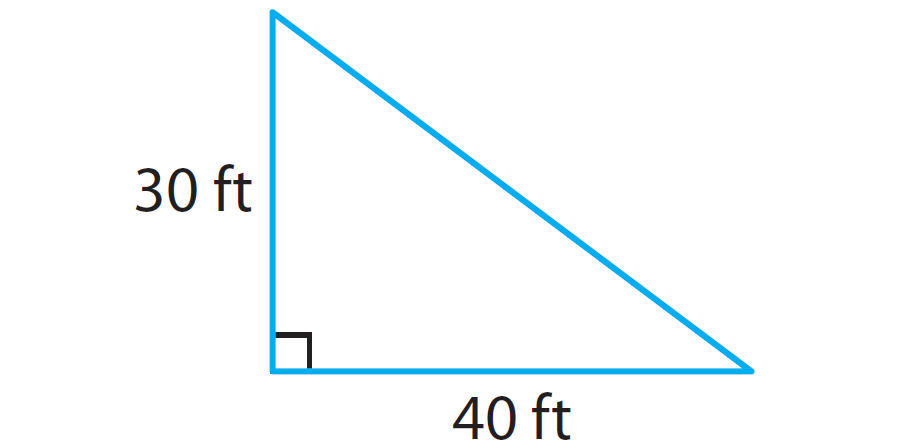
Problem 4 :

In the right triangle given below, find the length of the missing side using Pythagorean theorem. 

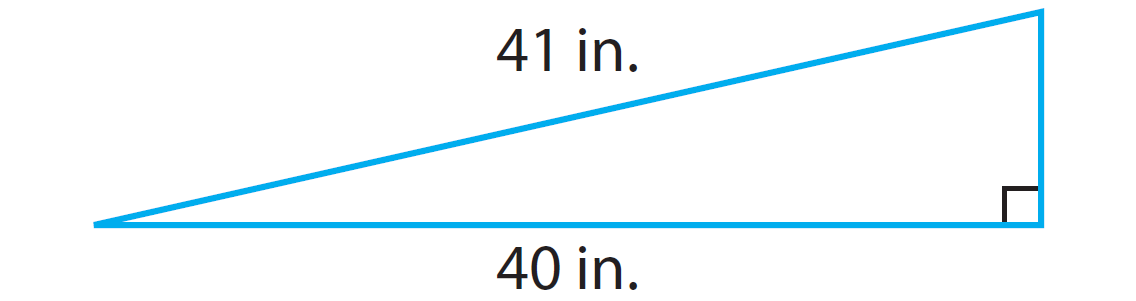
Answers

1. Answer :

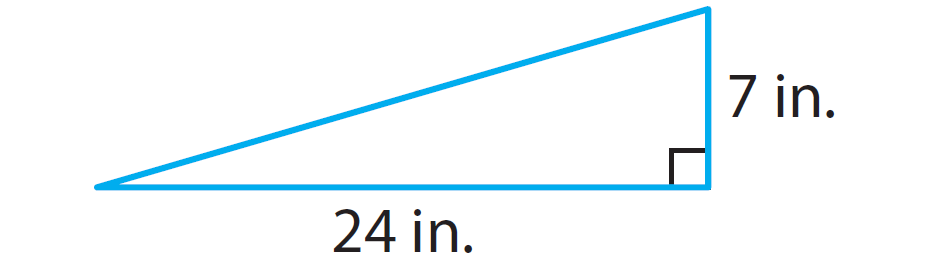
Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

Substitute the given measures.

7² + 24²  =  c²

Step 3 :

Solve the equation for c.

7² + 24²  =  c²

Simplify.

49 + 576  =  c²

625  =  c²

Write 625 as a perfect square (625  =  25²). 

25²  =  c²

Get rid of the square on both sides. 

25  =  c

Hence, the length of the hypotenuse is 25 inches.

2. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

Substitute the given measures.

a² + 12²  =  15²

Step 3 :

Solve the equation for c.

Simplify.

a² + 144  =  225

Subtract 144 from both sides. 

a²  =  81

Write 81 as a perfect square (81  =  9²). 

a²  =  9²

Get rid of the square on both sides. 

a  =  9

Hence, the length of the leg is 9 centimeters.

3. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

Substitute the given measures.

30² + 40²  =  c²

Step 3 :

Solve the equation for c.

30² + 40²  =  c²

Simplify.

900 + 1600  =  c²

2500  =  c²

Write 2500 as a perfect square (2500  =  50²). 

50²  =  c²

Get rid of the square on both sides. 

50  =  c

Hence, the length of the hypotenuse is 50 ft.

4. Answer :

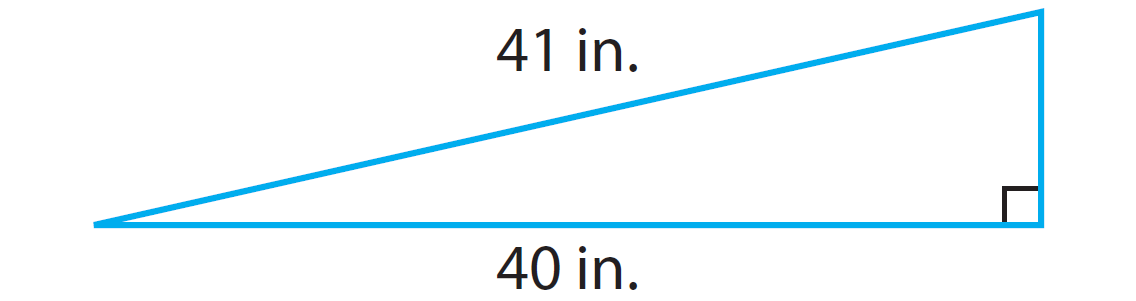
Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

Substitute the given measures.

a² + 40²  =  41²

Step 3 :

Solve the equation for c.

Simplify.

a² + 1600  =  1681

Subtract 1600 from both sides. 

a²  =  81

Write 81 as a perfect square (81  =  9²). 

a²  =  9²

Get rid of the square on both sides. 

a  =  9

Hence, the length of the leg is 9 inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.