USING REFERENCE ANGLES TO EVALUATE TRIGONOMETRIC FUNCTIONS

Using the reference angle to evaluate trigonometric functions.

Problem 1 :

sin 240°

Problem 2 :

cot 495°

Problem 3 :

sin 16π/3

Problem 4 :

sec (-π/4)

1. Answer :

The angle 240° has its terminal side in quadrant III, as shown in figure below.

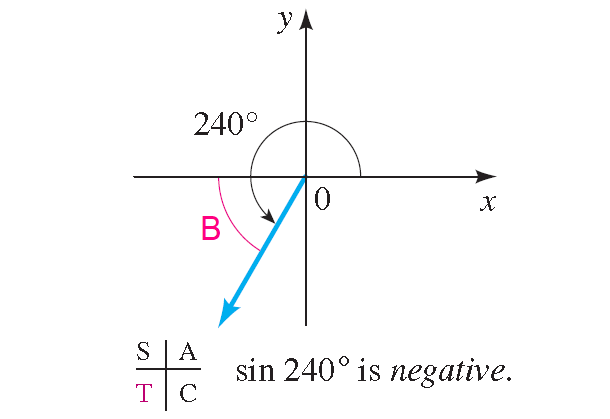
The reference angle is therefore

240° - 180°  =  60°,

and the value of sin 240° is negative. Thus

sin 240°  =  -sin 60°  =  √3/2

2. Answer :

The angle 495° is coterminal with the angle 135°, and the terminal side of this angle is in quadrant II, as shown in figure below.

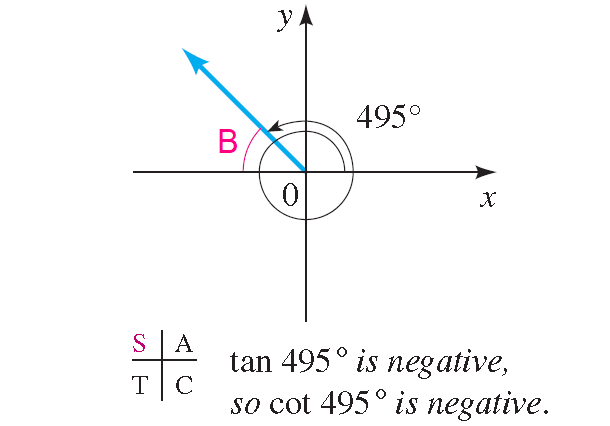
So the reference angle is

180° - 135°  =  45°,

and the value of cot 495° is negative. We have

cot 495°  =  cot 135°  =  -cot 45°  =  -1

3. Answer :

The angle 16π/3 is coterminal with 4π/3, and these angles are in quadrant III, as shown in the figure below.

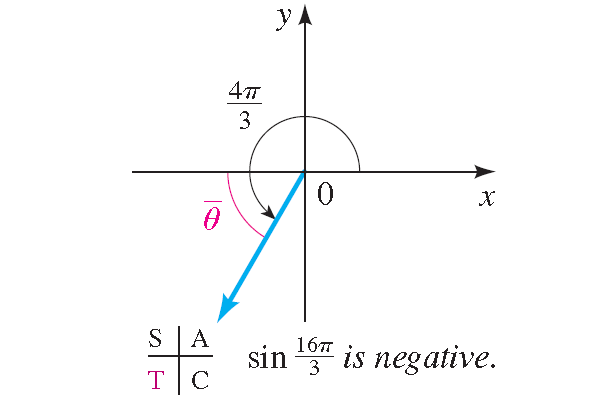
Thus, the reference angle is

4π/3 - π  =  π/3

Because the value of sine is negative in quadrant III, we have

sin 16π/3  =  sin 4π/3  =  -sin π/3  =  -√3/2

4. Answer :

The angle -π/4 is in quadrant IV, and its reference angle is π/4, as shown in the figure below.

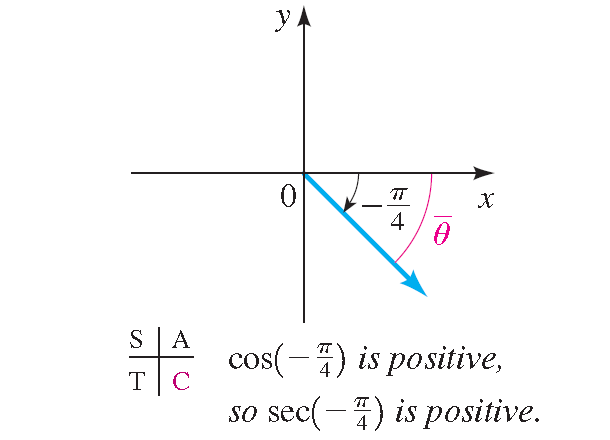
Because secant is positive in this quadrant, we get

sec (-π/4)  =  +sec (π/4)  =  √2/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.