USING REFERENCE NUMBERS TO FIND TERMINAL POINTS
Suppose t is a real number. If t ≥ 0, let's mark off a distance t along the unit circle, starting at the point (1, 0) and moving in a counterclockwise direction. If t < 0, we mark off a distance |t| in a clockwise direction.
In this way we arrive at a point (x, y) on a unit circle. The point P(x, y) obtained in this way is called the terminal point determined by a real number t.
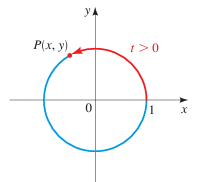
Terminal point P(x, y) determined by t > 0
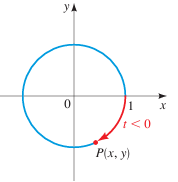
Terminal point P(x, y) determined by t < 0
How to find terminal point using reference number ?
To find the terminal point P determined by any value of t, we use the following steps:
Step 1 :
Find the reference number t.
Step 2 :
Find the terminal point Q(a, b) determined by t.
Step 3 :
The terminal point determined by t is P(±a, ±b), where the signs are chosen according to the quadrant in which this terminal point lies.
Find the terminal point determined by each given real number t.
Example 1 :
t = 3π
Solution :
The terminal point determined by 3π is (-1, 0)
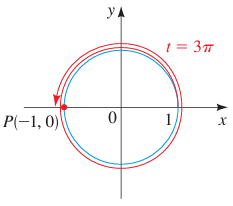
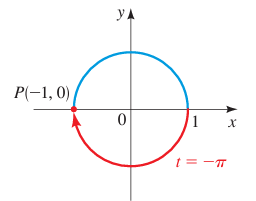
Example 2 :
t = -π
Solution :
The terminal point determined by -π is (-1, 0)
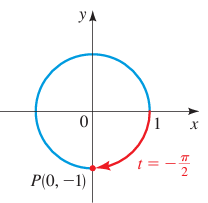
Example 3 :
t = -π/2
Solution :
The terminal point determined by -π/2 is (0, -1).
Example 4 :
t = π/4
Solution :
The terminal point P(x, y) determined by t = π/4 is the same distance from (1, 0) as from (0, 1) along the unit circle.
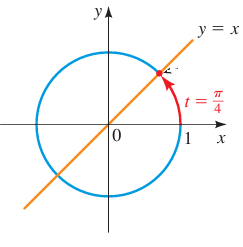
Since the unit circle is symmetric with respect to y = x, it follows that P lies on the line y = x. So, P is the point of intersection of the circle x2 + y2 = 1 and the line y = x.
x2 + y2 = 1
Here applying the value of y from y = x, we get
x2 + x2 = 1
2 x2 = 1
x2 = 1/2
x = √2/2
and y = √2/2
So, the required terminal point for t = π/4 is (√2/2, √2/2).
Example 5 :
t = -π/4
Solution :
The terminal point P(x, y) determined by t = π/4 is the same distance from (1, 0) as from (0, 1) along the unit circle. But the given angle measure is -π/4, then we go in counterclockwise direction.
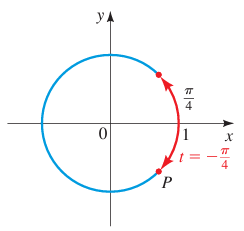
Since the required terminal point lies in the fourth quadrant, the point will be in the form (x, -y). So, the required point is (√2/2, -√2/2).
Example 6 :
t = 5π/6
Solution :
Given number = t = 5π/6
Reference number = π - 5π/6
= π/6
The reference number is t' = π/6, which determines the terminal point (√3/2, 1/2).
Because the terminal point determined by t is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus, the desired terminal point is
(-√3/2, 1/2)
Example 7 :
t = 7π/4
Solution :
Given number = t = 7π/4
Reference number = 2π - 7π/4
= π/4
The reference number is t' = π/4, which determines the terminal point (√2/2, √2/2).
Because the terminal point is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the desired terminal point is
(√2/2, -√2/2)
Example 8 :
t = -2π/3
Solution :
Given number = t = -2π/3
Reference number = π - 2π/3
= π/3
The reference number is t' = π/3, which determines the terminal point (1/2, √3/2).
Because the terminal point determined by t is in quadrant III, its both x-coordinate and y-coordinate are negative. Thus, the desired terminal point is
(-1/2, -√3/2)
Because the circumference of the unit circle is 2π, the terminal point determined by t is the same as that determined by (t + 2π) or (t - 2π). In general, we can add or subtract 2π any number of times without changing the terminal point determined by t. We can use this observation in the next example to find terminal points for large t.
Finding the Terminal Point for Large t
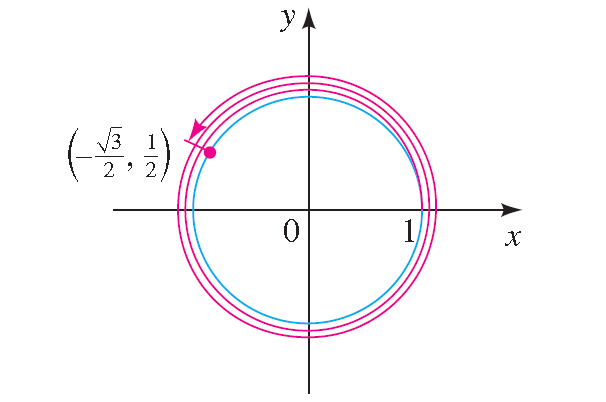
Example 9 :
Find the terminal point determined by t = 29π/6.
Solution :
Because
t = 29π/6 = 4π + 5π/6
we see that the terminal point of t is the same as that of 5π/6 (that is, we subtract 4π).
So by Example 13 the terminal point is
(-√3/2, 1/2)
Related Stuff
2. Terminal Points on the Unit Circle
3. Reference Number on the Unit Circle
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
