USING REMAINDER THEOREM EXAMPLES WITH ANSWERS

Find the remainder using remainder theorem, when

Example 1 :

3x³+4x²-5x+8 is divided by x-1.

Solution :

Let p(x) = 3x³+4x²-5x+8.  The zero of x-1 is 1.

When p(x) is divided by x-1, the remainder is p(1).

p(1)  =  3(1)³+4(1)²-5(1)+8

=  3+4-5+8   

=  10

The remainder is 10.

Example 2 :

5x³+2x²-6x+12 is divided by x+2.

Solution :

Let  p(x)  =  5x³+2x²-6x+12

The zero of x+2 is -2.

When p(x) is divided by x+2, the remainder is p(-2).

p(-2)  =  5(-2)³+2(-2)²-6(-2)+12

=  5(-8)+2(4)+12+12

=  40  + 8  + 12 + 12

=  -8

The remainder is -8.

Example 3 :

2x³-4x²+7x+6 is divided by x-2.

Solution :

Let p(x)  =  2x³-4x²+7x+6

The zero of x-2 is 2.

When p(x) is divided by x-2, the remainder is p(2).

p(2)  =  2(2)³-4(2)²+7(2)+6

=  2(8)-4(4)+14+6

=  16-16+14+6

=  20

The remainder is 20.

Example 4 :

4x³-3x²+2x-4 is divided by x+3

Solution :

Let p(x)  = 4x³-3x²+2x-4. The zero of x+3 is -3.

When p(x) is divided by x+3, the remainder is p(-3).

p(-3)  =  4(-3)³-3(-3)²+2(-3)-4

=  4(-27)-3(9)-6-4

=  -108 -27 -6-4

=  -145

The remainder is -145.

Example 5 :

4x³ - 12x² +11x -5 is divided by 2x-1

Solution :

Let p(x)  =   4x³ - 12x² +11x -5.  The zero of 2x-1 is 1/2.

When p(x) is divided by 2x-1, the remainder is p(1/2).

p(1/2)  =  4(1/2)³-12(1/2)² +11(1/2) -5

=  4(1/8) -12(1/4)+11/2-5

=  -2

The remainder is -2.

Example 6 :

8x⁴+12x³-2x²-18x +14 is divided by x+1

Solution :

Let p(x)  =   8x⁴+12x³-2x²-18x +14

The zero of x+1 is -1.

When p(x) is divided by x+1, the remainder is p(-1).

p(-1) =  8(-1)⁴+12(-1)³-2(-1)²-18(-1) +14

=  8-12-2+18+14

=  40-14

=  26

The remainder is 26.

Example 7 :

x³-ax² -5x+2a is divided by x-a.

Solution :

Let p(x)  = x³-ax² -5x+2a. The zero of x-a is a.

When p(x) is divided by x-a, the remainder is a.

p(a)  =  a³-a(a)² -5a+2a

=  a³-a³ -3a

=  -3a

The remainder is -3a. 

Example 8 :

When the polynomial

2x³-ax²+9x-8

is divided by x-3 the remainder is 28. Find the value of a.

Solution :

Let p(x)  =  2x³-ax²+9x-8

When p(x) is divided by x-3, the remainder is p(3).

Given that p(3)  =  28.

This implies that 2(3)³ - a(3)² + 9(3) -8.  =  28

2(27)-a(9)+27-8  =  28

54-9a+19  =  28

73-9a  =  28

73-28  =  9a    

45  =  9a 

a  =  5

So, the value of a is 5.

Example 9 :

Find the value of m if

x³-6x²+mx+60

leaves the remainder 2 when divided by (x+2).

Solution :

Let p(x)  =  x³-6x²+mx+60

When p(x) is divided by (x+2) the remainder is p(-2).

Given that p(-2)  =  2

This implies that (-2)³-6(-2)²+m(-2)+60  =  2

-8-6(4)-2m+60  =  2

-8-24-2m+60  =  2

28-2m  =  2 

28-2  =  2m

26  =  2m

m  =  13

Example 10 :

If (x-1) divides

mx³-2x²+25x-26

without remainder find the value of m.

Solution :

Let p(x)  =  mx³-2x²+25x-26

When p(x) is divided by (x-1), the remainder is p(1).

Given that p(1) = 0

This implies that m(1)³-2(1)²+25(1)-26  =  0

m-2+25-26  =  0

m-3  =  0

m  =  3

Example 11 :

If the polynomials

x³+3x²-m and 2x³-mx+9

leave the same remainder when they are divided by (x-2), find the value of m. Also find the remainder.

Solution :

Let p(x)  =  x³+3x²-m

q(x)  =  2x³-mx+9

When p(x) is divided by (x-2) the remainder is p(2). Now,

p(2)  =  2³+3(2)²-m

=  8+12-m   

=  20 - m  --------(1)

When q(x) is divided by (x-2) the remainder is q(2).  Now,

q(2)  =  2(2)³-m(2)+9

=  16-2m+9

=  25-2m   --------(2)

Given that p(2)  =  q(2).  That is 

20 - m  =  25 - 2m 

2m - m  =  25 - 20

m  = 5

By applying the value of m in (1), we get

=  20 -5

=  15. 

The remainder is 15.

Example 12 :

For a polynomial p(x), the value of of p(3) is -2, which of the following must be true about p(x) ?

a)  x - 5 is a factor of f(x)

b)  x - 2 is a factor of f(x) 

c) x + 2 is a factor of f(x)

d) the remainder when p(x) is divided by x - 3 is -2

Solution :

For a polynomial p(x),

• When p(a) = 0, then x = a is a solution and x - a is a factor.
• When p(a) ≠ 0, then x = a is not a solution and x - a is not a factor.
  
• When p(a) = b, then x = a is not a solution and x - a is not a factor and b is the remainder.

So, option d is correct.

Example 13 :

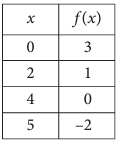
The function f is defined by a polynomial, some values of x and f(x) are shown in the table above. Which of the following must be a factor of f(x) ?

a)  x - 2    b)  x - 3     c)  x - 4   d)  x - 5

Solution :

By observing the table, when x = 4 the remainder is 0.

That is, f(4) = 0

then x - 4 is a factor.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.