USING SIMILAR TRIANGLES TO FIND SLOPE WORKSHEET

Problem 1 : 

In the diagram given below, using similar triangles, prove that the slope between the points D and F is the same as the slope between the points A and C.

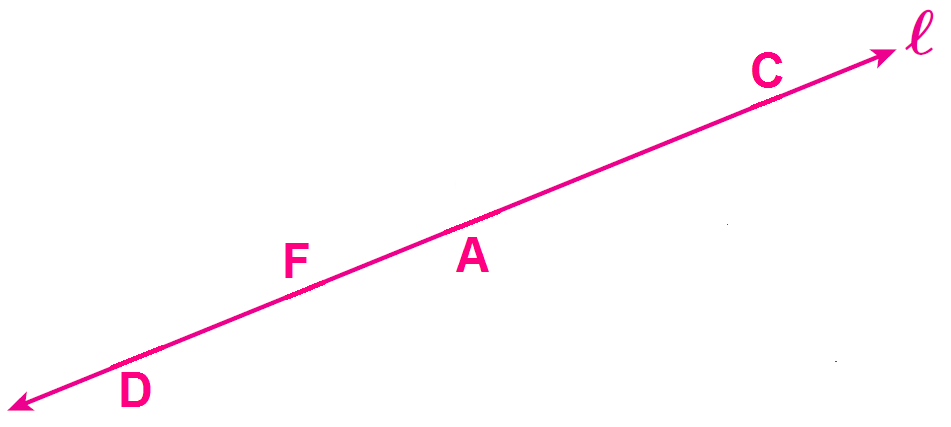
Problem 2 : 

Suppose that we label two other points on line ℓ as P and Q. Would the slope between these two points be different than the slope we found in the above activity ? Explain.

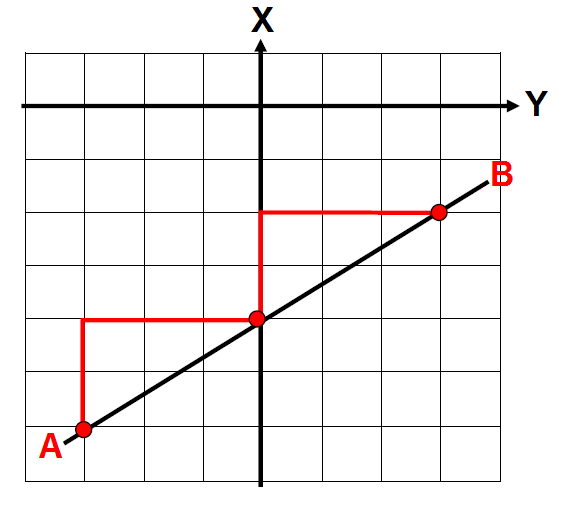
Problem 3 : 

Find the slope of the line AB using the similar triangles as a guide.

Detailed Answer Key

Problem 1 : 

In the diagram given below, using similar triangles, prove that the slope between the points D and F is the same as the slope between the points A and C.

Solution :

Step 1 :

Draw the rise and run for the slope between points D and F. Label the intersection as point E. Draw the rise and run for the slope between points A and C. Label the intersection as point B.

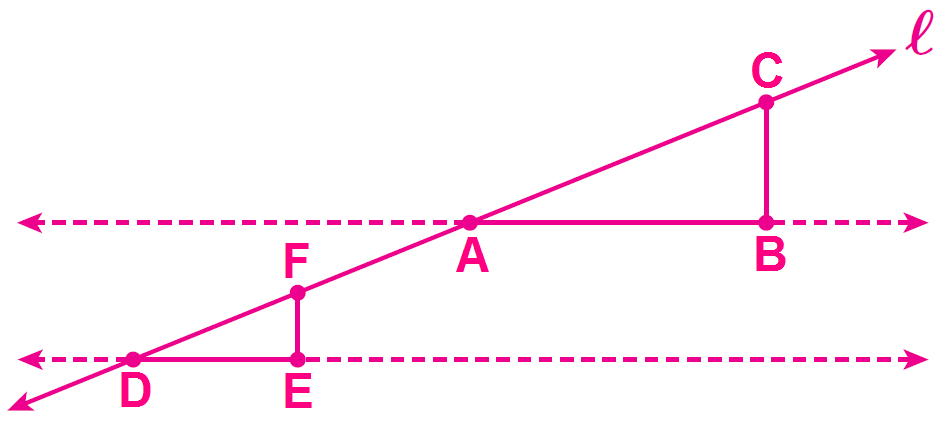
Step 2 :

Write expressions for the slope between D and F and between A and B. 

Slope between D and F :  FE / DE

Slope between A and B :  CB / AB

Step 3 :

Extend DE and AB across our drawing. DE and AB are both horizontal lines, so they are parallel.

Line l is a transversal that intersects parallel lines.  

Step 4 :

Because DE and AB are parallel lines and ℓ is a transversal that intersects DE and AB, 

m∠FDE and m∠CAB are corresponding angles and they are congruent. 

m∠FED and m∠CBA are right angles and they are congruent. 

Step 5 :

By Angle–Angle Similarity, triangle ABE and triangle CDF are similar triangles. 

Step 6 :

Because triangle ABE and CDF are similar, the lengths of corresponding sides of similar triangles are proportional.

FE / CB  =  DE / AB

Step 7 :

Recall that you can also write the proportion so that the ratios compare parts of the same triangle :

FE / DE  =  CB / AB

Step 8 :

The proportion we wrote in step 8 shows that the ratios we wrote in step 2 are equal. So, the slope of line ℓ is constant.

Hence, the slope between the points D and F is the same as the slope between the points A and C.

Problem 2 :

Suppose that we label two other points on line ℓ as P and Q. Would the slope between these two points be different than the slope we found in the above activity ? Explain.

Solution

No

The slope of the line is constant, so the slope between the points P and Q would be the same. Moreover, not only the two points P and Q, between any two points on ℓ, the slope would be same. 

Problem 3 :

Find the slope of the line AB using the similar triangles as a guide.

Solution :

Step 1 :

Slope is a ratio between the change in y and the change in x. That is  y/x.

Step 2 : 

Both triangles rise 2 places (y) and run 3 places (x). So the slope is 2/3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.