USING SIMILAR TRIANGLES TO FIND THE MEASURE OF X

Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion. In other words, similar triangles are the same shape, but not necessarily the same size.

Example 1 :

Given that BC is 3 m longer than AB, find the height of the flag pole.

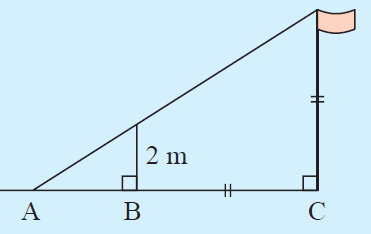
Solution :

Let x be length of AB.

BC  =  x + 3

In the picture given above, we have two triangles.

Since the two triangles are equiangular, they are similar.

Here length of pole  =  BC  =  x + 3

Using the concept of similar triangle,

2/x  =  (x+3)/(x+x+3)

2/x  =  (x+3)/(2x+3)

2(2x+3)  =  x(x+3)

4x+6  =  x²+3x

 x²+3x-4x-6  =  0

 x²-x-6  =  0

(x+2)(x-3)  =  0

x  =  -2 and x  =  3

x+3  ==>  3+3  ==>  6

So, height of the flag pole is 6 m.

Example 2 :

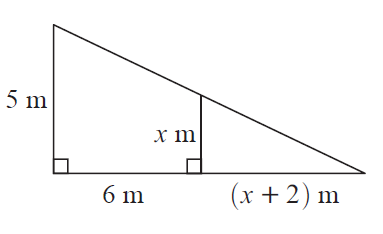
Solution :

5/(6+x+2)  =  x/(x+2)

5/(8+x)  =  x/(x+2)

5(x+2)  =  x(8+x)

5x+10  =  8x+x²

x² + 3x - 10  =  0

(x+5)(x-2)  =  0

x  =  -5 and x  =  2

-5 is not possible. So, value of x is 2.

Example 3 :

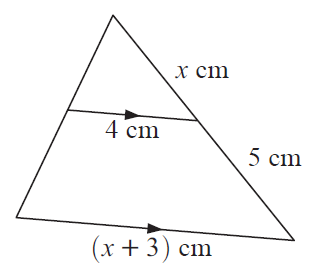
Solution :

x/4  =  (x+5)/(x+3)

x(x+3)  =  4(x+5)

x²+3x  =  4x+20

x²+3x-4x-20  =  0

x²-x-20  =  0

(x-5)(x+4)  =  0

x  =  5 and x  =  -4

So, the value of x is 5.

Example 4 :

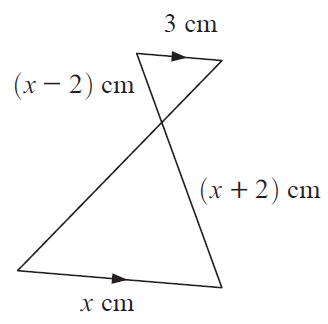
Solution :

3/(x-2)  =  x/(x+2)

3(x+2)  =  x(x-2)

3x+6  =  x²-2x

x²-2x-3x-6  =  0

x²-5x-6  =  0

(x-6)(x+1)  =  0

x  =  6 and x  =  -1

So, the value of x is 6.

Example 5 :

A, B, C and D are posts on the banks of a 20 m wide canal. A and B are 1 m apart. If OA = CD, find how far C and D are apart.

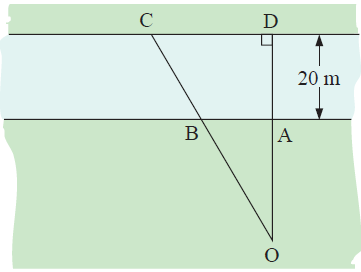
Solution :

Let OA  =  x

OA/AB = OD/CD

x/1 = (x+20)/x

x² = x+20

x² - x + 20  =  0

(x+5)(x-4)  =  0

x  =  -5 and x  =  4

So, C and D are 4 m apart.

Example 6 :

AB is 2 cm longer than BE. DC is 3 cm less than twice the length of BE.

a) Explain why triangles ABE and ACD are similar.

b) If BE = x cm, show that x²-4x-6  =  0.

c) Hence, show that BE = 2+√10 cm.

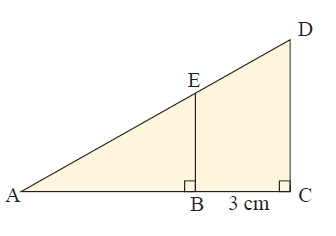
Solution :

Given :

Triangles ABE and ACF are similar.

If BE  =  x, AB  =  x+2, CD  =  2x-3

AB/BE  =  AC/CD

(x+2)/x  =  (x+2+3)/(2x-3)

(x+2)/x  =  (x+5)/(2x-3)

(x+2)(2x-3)  =  x(x+5)

2x²-3x+4x-6  =  x²+5x

2x²+x-5x-6  =  0

2x²-4x-6  =  0

x²-2x-3  =  0

(x-3)(x+1)  =  0

x  =  3 and x  =  -1

So, the value of x is 3.

Example 7 :

Quadrilateral P′Q′R′S′ is similar to quadrilateral PQRS, where P, Q, R, and S correspond to P′, Q′, R′, and S′, respectively. The measure of angle P is 30°, the measure of angle Q is 50°, and the measure of angle R is 70°. The length of each side of P′Q′R′S′ is 3 times the length of each corresponding side of PQRS. What is the measure of angle P′ ?

A) 10°    B) 30°    C) 40°    D) 90°

Solution :

Corresponding angle of P is P'

<P = 30° then <P' is also 30°

Example 8 :

A can has a height of 10 cm and has a volume of 200 cm³. A can with a similar shape has a height of 12 cm.

(a) Find the volume of the larger can.

(b) Find the height of a similar can with a volume of 675 cm³.

Solution :

Height of small cone = 10 cm

Volume = 200 cm³

Height of large cone = 12 cm

Volume = ?

a)  

Since these two cones are similar, 

(Volume of large cone/Volume of small cone)

= (Height of large cone / height of small cone)³

(volume of large cone/200) = (12/10)³

(volume of large cone/200) = 1.728

Volume of large cone = 200(1.728)

= 345.6 cm

b) Volume of large cone = 675, then volume of the small cone = ?

(Volume of large cone/Volume of small cone)

= (Height of large cone / height of small cone)³

(675/Volume of small cone) = (12/10)³

(675/Volume of small cone) = 1.728

Volume of small cone = 675/1.728

= 390.625 cm³

Example 9 :

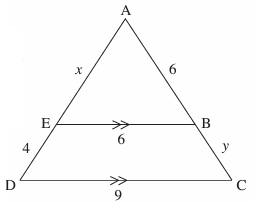
(a) Explain why triangles ABE and ACD are similar.

(b) Find the lengths of x and y.

Solution :

a)

Considering triangles, AEB and ADC

EB and DC are parallel.

<AEB = <ADC (Angle)

<EAB = <DAC (Angle)

Using AA, we say triangles AEB and ADC are similar. If two shapes are similar, then the corresponding sides will be in the same ratio.

AE/AD = AB/AC = EB/DC

x/(x + 4) = 6/(6 + y) = 6/9

b)

Finding the value of x :

x/(x + 4) = 6/9

9x = 6(x + 4)

9x = 6x + 24

9x - 6x = 24

3x = 24

x = 24/3

x = 8

Finding the value of y :

y/(6 + y) = 6/9

9y = 6(6 + y)

9y = 36 + 6y

9y - 6y = 36

3y = 36

y = 36/3

y = 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.