USING SLOPE INTERCEPT FORM TO GRAPH A LINE

Example 1 :

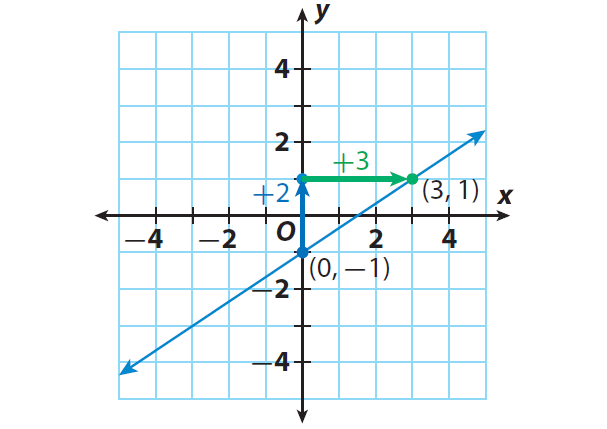
Graph the line whose equation is y = (2/3)x - 1.

Solution :

Step 1 :

The y-intercept is b = -1. Plot the point that contains the y-intercept : (0, -1).

Step 2 : 

The slope is m = 2/3. Use the slope to find second a point. Since the slope  =  rise / run, from (0, -1), count up 2 units and right 3 units. 

Then, the new point is (3, 1). 

Step 3 : 

Draw a line through the points. 

Example 2 :

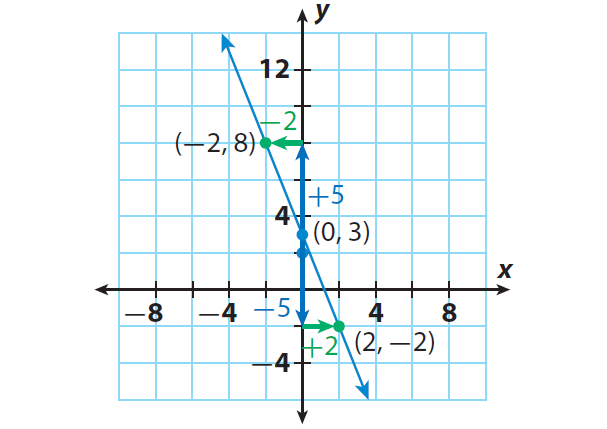
Graph the line whose equation is y = (-5/2)x + 3.

Solution :

Step 1 :

The y-intercept is b = 3. Plot the point that contains the y-intercept : (0, 3).

Step 2 : 

The slope is m = -5/2. Use the slope to find second a point. Since the slope  =  rise / run, from (0, 3), count down 5 units and right 2 units or up 5 units and left 2 units. 

Then, the new point is (2, -1) or (-2, 8). 

Step 3 : 

Draw a line through the points. 

Example 3 :

Ken has a weekly goal of burning 2400 calories by taking brisk walks. The equation y = -300x + 2400 represents the number of calories y Ken has left to burn after x hours of walking which burns 300 calories per hour. After how many hours of walking will Ken have 600 calories left to burn ? After how many hours will he reach his weekly goal?

Solution :

Step 1 :

 y = -300x + 2400

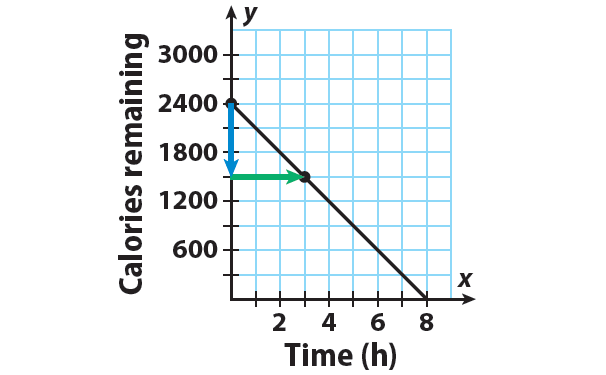
The y-intercept is b = 2400. Plot the point that contains the y-intercept : (0, 2400).

Step 2 :

Write the slope as a fraction.

m = -300/1

= -600/2

= -900/3

Using the slope as -900/3 helps in drawing a more accurate graph.

The slope is m = -900/3. Use the slope to find second a point. Since the slope  =  rise / run, from (0, 2400), count down 900 units and right 3 units. 

Then, the new point is (3, 1500). 

Step 3 :

Draw a line through the points. 

Step 4 :

To find after how many hours of walking will Ken have 600 calories left to burn, 

Locate 600 calories on the y-axis. Read across and down to the x-axis.

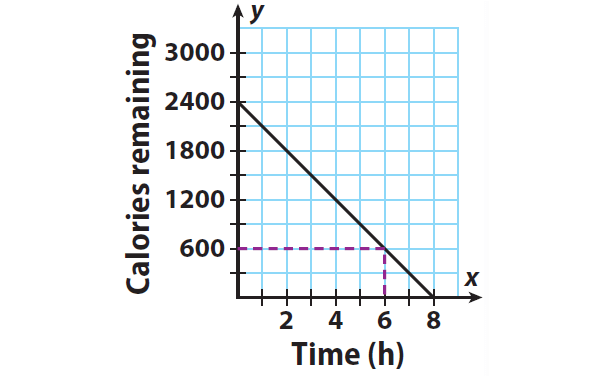
From the graph, we can know that Ken will have 600 calories left to burn after 6 hours.

Step 5 :

Ken will reach his weekly goal when the number of calories left to burn is 0. Because every point on the x-axis has a y-value of 0, find the point where the line crosses the x-axis.

Ken will reach his goal after 8 hours of brisk walking.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.