USING SLOPE TO COMPARE UNIT RATES WORKSHEET

Problem 1 :

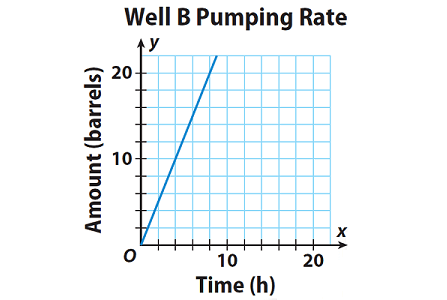
The equation y  =  2.75x represents the rate, in barrels per hour, that oil is pumped from Well A. The graph represents the rate that oil is pumped from Well B. Which well pumped oil at a faster rate?

Problem 2 :

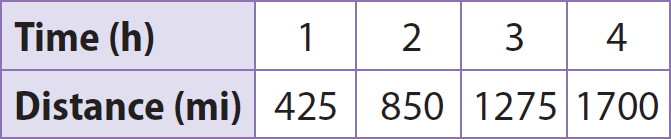
The equation y = 375x represents the relationship between x, the time that a plane flies in hours, and y, the distance the plane flies in miles for Plane A. The table represents the relationship for Plane B. Find the slope of the graph for each plane and the plane’s rate of speed. Determine which plane is flying at a faster rate of speed.

Answers

1. Answer :

Step 1 :

Use the equation y = 2.75x to make a table for Well A’s pumping rate, in barrels per hour.

Step 2 :

Use the table to find the slope of the graph of Well A.

Slope = Unit rate

= (5.5 - 2.75)/(2 - 1)

= 2.75/1

= 2.75 barrels/hour

Step 3 :

Use the graph to find the slope of the graph of Well B.

Slope = Unit rate

= rise/run

= 10/4

= 2.5 barrels/hour

Step 4 :

Compare the unit rates.

2.75 > 2.5

So Well A’s rate, 2.75 barrels/hour, is faster.

2. Answer :

Step 1 :

Use the equation y = 375x to find the slope of the graph of Plane A.

Slope = Unit rate

Here, unit rate is the distance covered by the plane in one hour.

To find unit rate, substitute x = 1 in y = 375x.

Slope = 375(1)

= 375 miles/hour

Step 2 :

Use the table to find the slope of the graph of Plane B.

Slope = Unit rate

= (850 - 425)/(2 - 1)

= 425/1

= 425 miles/hour

Step 3 :

Compare the unit rates.

425 > 375

So, Plane B is flying faster.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.