USING THE AA SIMILARITY POSTULATE

Similar figures have the same shape but may have different sizes. We can determine whether two triangles are similar by using the AA similarity postulate. 

Angle-Angle (AA) Similarity Postulate

If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

Solved Problems

Problem 1 : 

Using AA similarity postulate, determine whether the triangles PQR and STU  are similar.

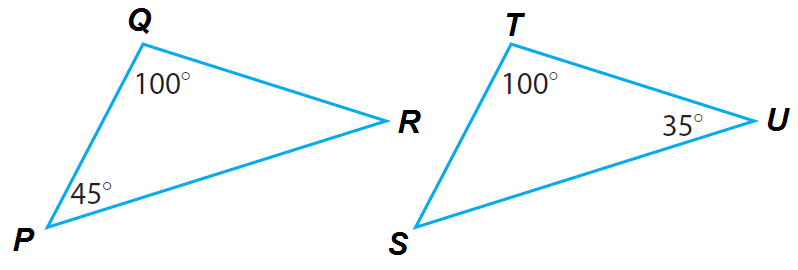
Solution :

The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle PQR : 

Write the Triangle Sum Theorem for this triangle.

m∠P + m∠Q + m∠R  =  180°

Substitute the given angle measures.

45° + 100° + m∠R  =  180°

Simplify.

145° + m∠R  =  180°

Subtract 145° from both sides.

145° + m∠R - 145°  =  180° - 145°

Simplify.

m∠R  =  35°

Triangle STU : 

Write the Triangle Sum Theorem for this triangle.

m∠S + m∠T + m∠U  =  180°

Substitute the given angle measures.

m∠S + 100° + 35°  =  180°

Simplify.

m∠S + 135°  =  180°

Subtract 135° from both sides.

m∠S + 135° - 135°  =  180° - 135°

Simplify.

m∠S  =  45°

Conclusion :

Three Angles of triangle PQR are 45°, 100° and 35°.

Three Angles of triangle STU are 45°, 100° and 35°.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Problem 2 : 

Using AA similarity postulate, determine whether the triangles ABC and DEF  are similar.

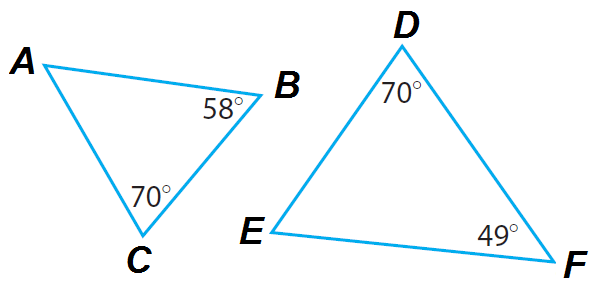
Solution :

The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle ABC : 

Write the Triangle Sum Theorem for this triangle.

m∠A + m∠B + m∠C  =  180°

Substitute the given angle measures.

m∠A + 58° + 70°  =  180°

Simplify.

m∠A + 128°  =  180°

Subtract 128° from both sides.

m∠A + 128° - 128°  =  180° - 128°

Simplify.

m∠A  =  52°

Triangle DEF : 

Write the Triangle Sum Theorem for this triangle.

m∠D + m∠E + m∠F  =  180°

Substitute the given angle measures.

70° + m∠E + 49°  =  180°

Simplify.

m∠E + 119°  =  180°

Subtract 119° from both sides.

m∠E + 119° - 119°  =  180° - 119°

Simplify.

m∠E  =  61°

Conclusion :

Three Angles of triangle ABC are 52°, 58° and 70°.

Three Angles of triangle DEF are 70°, 61° and 49°.

Because only one angle is congruent, the two triangles are not similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.