USING TRANSLATION VECTORS TO TRANSFORM FIGURES WORKSHEET
Problem 1 :
Find the image equation when 3x + 2y = 8 is translated under the vector <-1, 3>
Problem 2 :
Find the image equation when 2x - y = 6 is translated under the vector <-3, 0>
Problem 3 :
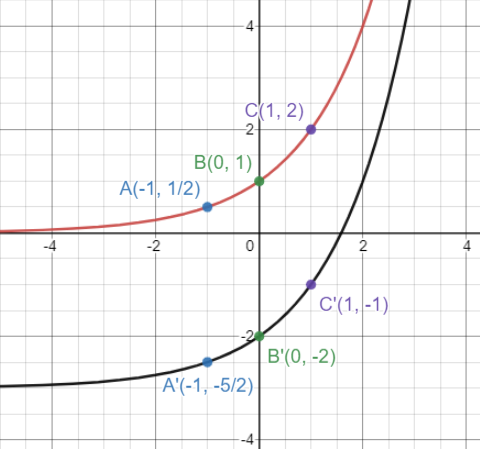
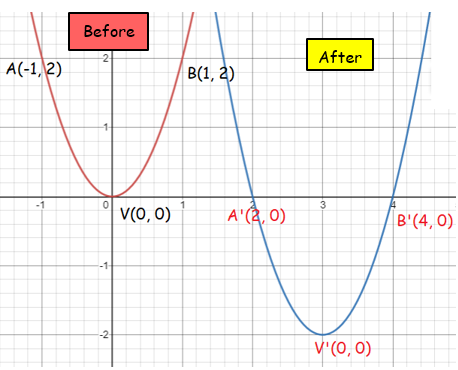
Find the image equation when y = x2 is translated under the vector <0, 3>
Problem 4 :
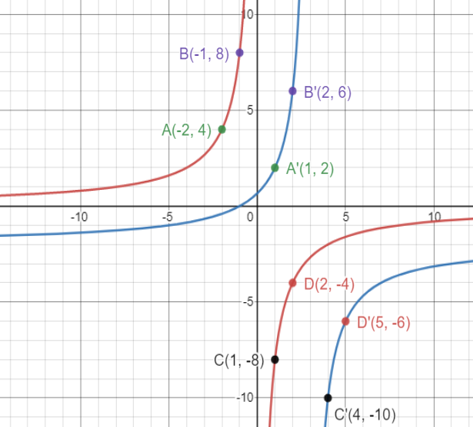
Find the image equation when xy = -8 is translated under the vector <3, -2>
Problem 5 :
Find the image equation when y = 2x is translated under the vector <0, -3>
Problem 6 :
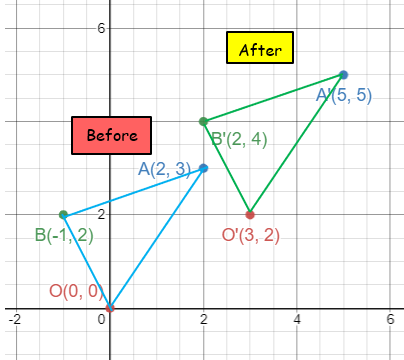
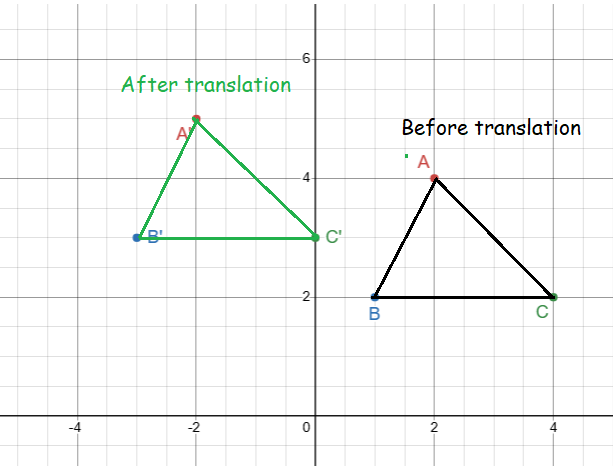
Triangle OAB with vertices O(0, 0), A(2, 3) and B(-1, 2) is translated under the vector <3, 2>. Find the image vertices and illustrate the object and the image.
Problem 7 :
Find the image equation when 2x - 3y = 6 is translated under the vector <-1, 2>
Problem 8 :
Find the image of y = 2x2 under a translation with vector <3, -2>.
Problem 9 :
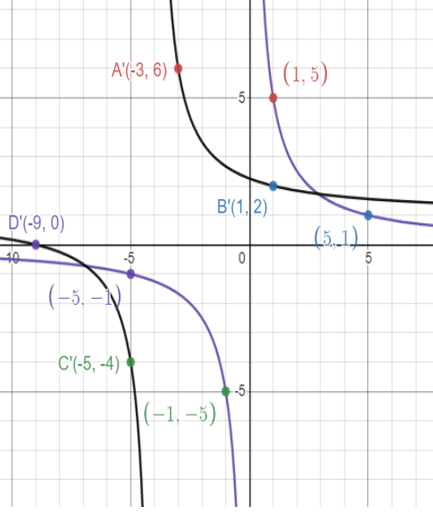
Find the image of xy = 5 under a translation with vector <-4, 1>

(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
Problem 1 :
Triangle OAB with vertices O(0, 0), A(2, 3) and B(-1, 2) is translated under the vector <3, 2>. Find the image vertices and illustrate the object and the image.
Problem 2 :
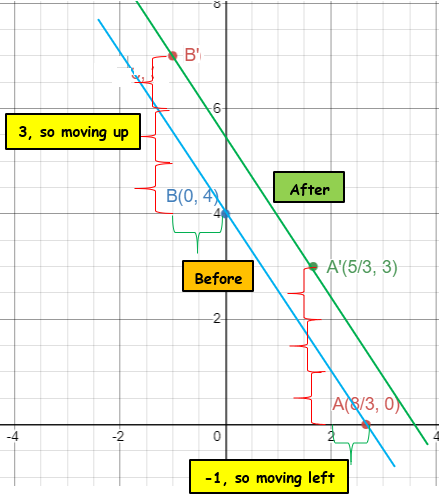
Find the image equation when 2x - 3y = 6 is translated under the vector <-1, 2>.
Problem 3 :
Find the image of y = 2x2 under a translation with vector <3, -2>.
Problem 4 :
Find the image of xy = 5 under a translation with vector <-4, 1>.
Problem 5 :
Draw the preimage and image of each triangle under a translation along (-4, 1).
Problem 6 :
Triangle with coordinates
A (2, 4) B (1, 2) and C (4, 2).
Problem 7 :
A translation along the vector 〈−2, 7〉 maps point P to point Q. The coordinates of point Q are (4, −1) . What are the coordinates of point P? Explain your reasoning.
Problem 8 :
Find the coordinates of the image under the transformation ⟨6, -11⟩.
a) (x, y) ==> b) (2, -3) ==>
c) (3, 1) ==> d) (4, -3) ==>
Answer Key
1)
- O(0, 0) ==> O'(3, 2)
- A(2, 3) ==> A'(5, 5)
- B(-1, 2) ==> B'(2, 4)

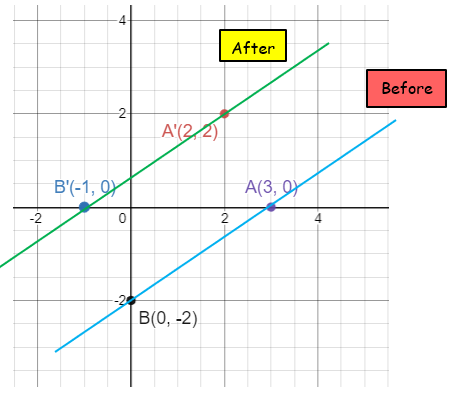
2)
- A(3, 0) ==> A'(2, 2)
- B(0, -2) ==> B'(-1, 0)

3) y = 2x2 - 12x + 16

4) xy - 4x + 4y - 9 = 0

5)
- A(2, 4) ==> A'(-2, 5)
- B(1, 2) ==> B'(-3, 3)
- C(4, 2) ==> C'(0, 3)
6) the required point is P(6, -8)
7)
- a) (x, y) ==> (x + 6, y - 11)
- b) (2, -3) ==> (8, -14)
- c) (3, 1) ==> (9, -10)
- d) (4, -3) ==> (10, 8)
Problem 1 :
Find the image equation when 3x + 2y = 8 is translated under the vector <-1, 3>.
Problem 2 :
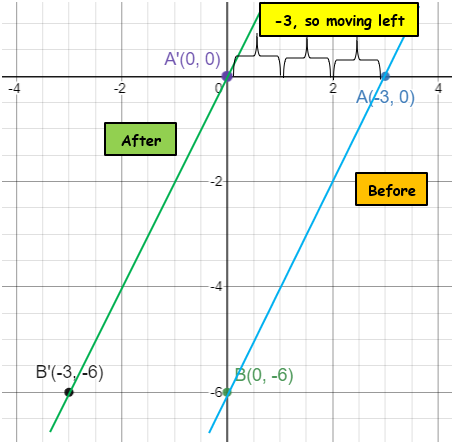
Find the image equation when 2x - y = 6 is translated under the vector <-3, 0>.
Problem 3 :
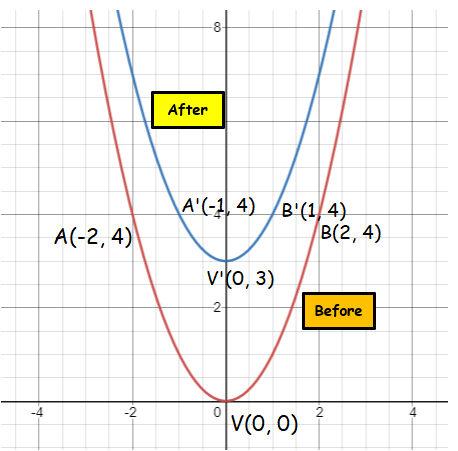
Find the image equation when y = x2 is translated under the vector <0, 3>.
Problem 4 :
Find the image equation when xy = -8 is translated under the vector <3, -2>.
Problem 5 :
Find the image equation when y = 2x is translated under the vector <0, -3>.
Problem 6 :
A trapezoid is translated 7 units to the right and then reflected across the x-axis.
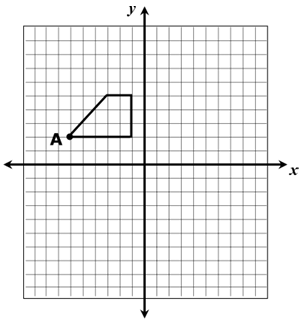
Which ordered pair describes the image of point A ?
a) (1, 2) b) (1, -2) c) (-1, 2) d) (-6, -5)
Problem 7 :
Which expression describes the translation of a point from (-3, 4) to (4, -1).
a) 7 units left and 5 units up.
b) 7 units right and 5 units up.
c) 7 units left and 5 units down
d) 7 units right and 5 units down.
Problem 8 :
The vertices of triangle ABC are (2, 1), B (3, 4) and C(1, 3). If triangle is translated 1 unit down and 3 units left to create triangle DEF, what are the coordinated of triangle DEF?
Answer Key
1)

2)

3)

4)

5)

6) A'(1, -2), option c
7) 7 units right and 5 units down.
8)
- A(2, 1) ==> A'(1, 4)
- B (3, 4) ==> B'(2, 7)
- C(1, 3) ==> C'(0, 6)
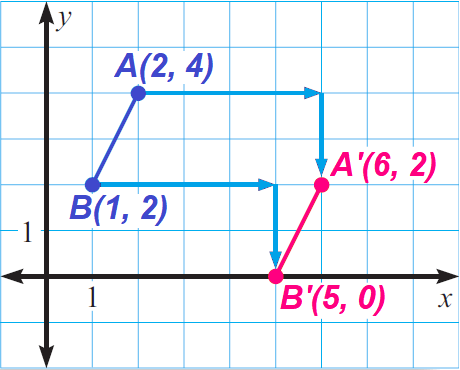
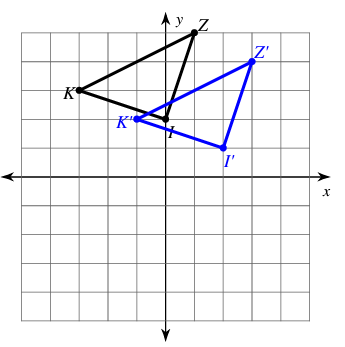
Problem 1 :
Describe the translation in the coordinate plane shown below.
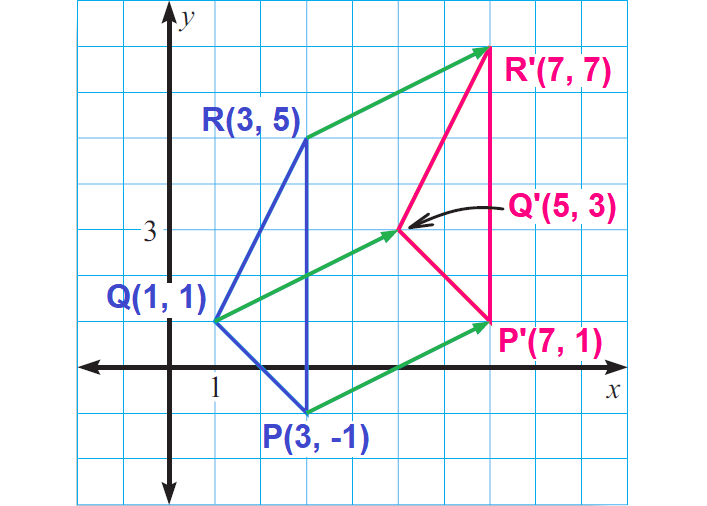
Problem 2 :
Sketch a triangle with vertices P(3, -1), Q (1, 1) and R(3, 5). Then sketch the image of the triangle after a translation to the right by 4 units and up by 2 units
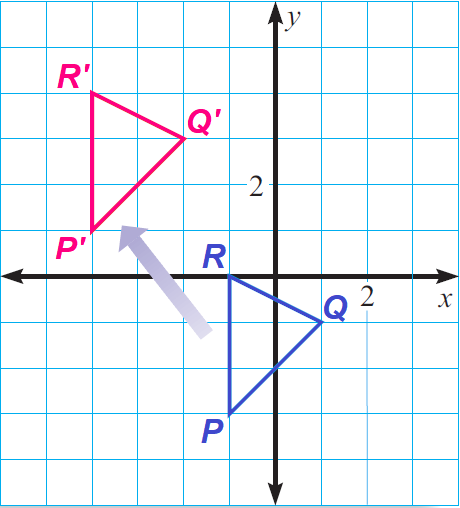
Problem 3 :
Sketch a triangle with vertices A(- 1, - 3), B(1, - 1), and C( - 1, 0). Then sketch the image of the triangle after the translation (x, y) ----> (x - 3, y + 4).
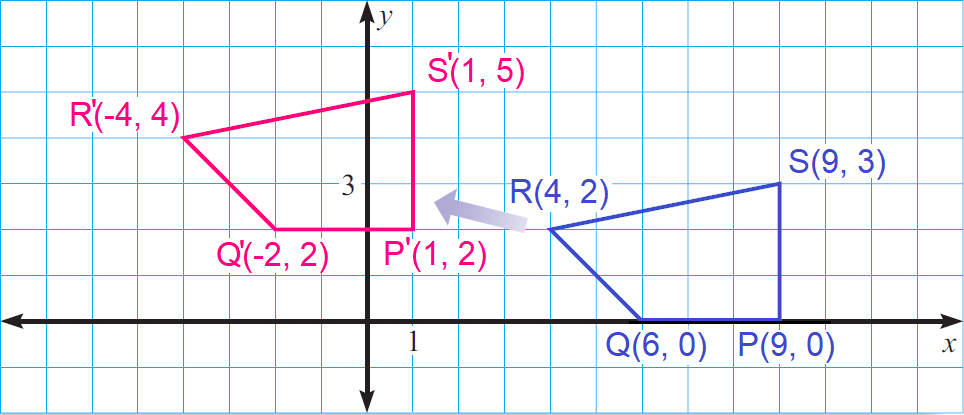
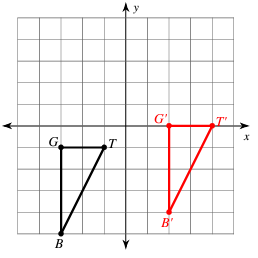
Problem 4 :
In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.
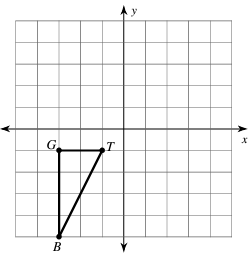
Problem 5 :
Graph the image of the figure using the transformation given.
translation: 5 units right and 1 unit up
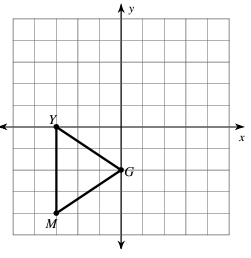
Problem 6 :
translation: 1 unit left and 2 units up
Example 7 :
Write a rule to describe each transformation.
Answer Key
1) the translation in the coordinate plane above shifts each point 4 units to the right and 2 units down.
2)
3)
4)
the component form of the vector is
〈-8, 2〉
5)
- G (-3, -1) ==> G'(2, 0)
- T (-1, -1) ==> T'(4, 0)
- B (-3, -5) ==> T'(2, -4)
6)
- G (-3, 0) ==> G'(-4, 2)
- G (0, -2) ==> G'(-1, 0)
- T (-3, -4) ==> T'(-4, -2)
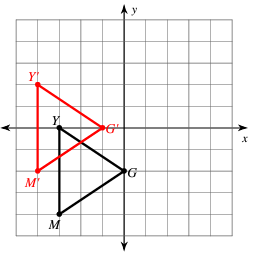
7) Moving the graph 2 units right and 1 unit down.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 04, 25 10:29 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 96)
Jan 04, 25 10:26 AM
Digital SAT Math Problems and Solutions (Part - 96) -
Simplifying Complex Fractions Problems and Solutions
Jan 04, 25 12:31 AM
Simplifying Complex Fractions Problems and Solutions