VERIFYING DEMORGANS LAWS WITH GIVEN SETS

Question 1 :

If A = {x : x ∊ Z,−2 < x ≤ 4}, B={x : x ∈ W, x ≤ 5}, C = {−4,−1, 0,2, 3, 4}, then verify A U (B n C) = (A U B) n (A U C).

Solution :

A  =  {x : x ∊ Z,−2 < x ≤ 4}

A  =  {-1, 0, 1, 2, 3, 4}

B  =  {x : x ∈ W, x ≤ 5}

B  =  {0, 1, 2, 3, 4, 5}

C = {−4,−1, 0, 2, 3, 4}

A U (B n C) = (A U B) n (A U C)

(B n C)  =  {0, 2, 3, 4}   

A U (B n C)  =  {-1, 0, 1, 2, 3, 4} ----(1)

(A U B)  =  {-1, 0, 1, 2, 3, 4, 5}

(A U C)  =  {-4, -1, 0, 1, 2, 3, 4}

(A U B) n (A U C)  =  {-1, 0, 1, 2, 3, 4}----(2)

(1)  =  (2)

Question 2 :

Verify A U (B n C) = (A U B) n (A U C) using Venn diagrams

Solution :

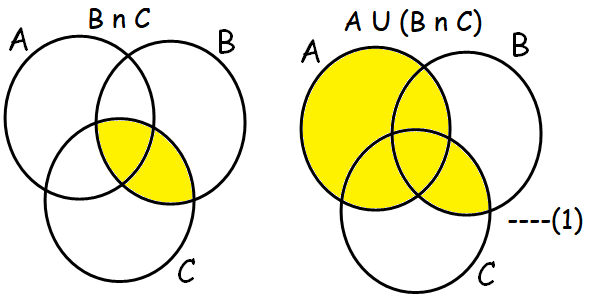
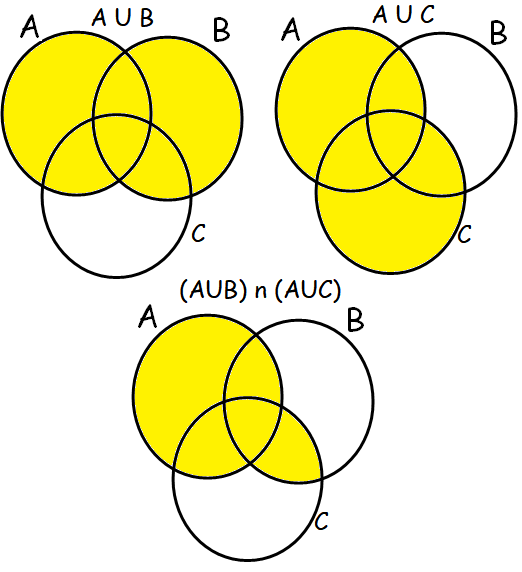
Hence proved.

Question 3 :

If A = {b, c, e, g, h} , B = {a, c, d, g, i} and C = {a, d, e, g, h} then show that A − (B n C) = (A − B) U (A−C) .

Solution :

(B n C)  =  {a, d, g}

A - (B n C)  =  {b, c, e, h}  ----(1)

(A − B)  =  {b, e, h}

(A − C)  =  {b, c}

(A − B) U (A−C)  =  {b, c, e, h}  ----(2)

(1)  =  (2)

Hence proved

Question 4 :

If A = {x : x = 6n, n ∈ W and n < 6}, B = {x : x = 2n, n ∈ N and 2 < n ≤ 9} and C = {x : x = 3n, n ∈ N and 4 ≤ n < 10}, then show that A−(B n C) = (A − B) U (A − C)

Solution :

A = {x : x = 6n, n ∈ W and n < 6}

A = {0, 6, 12, 18, 24, 30}

B = {x : x = 2n, n ∈ N and 2 < n ≤ 9}

B  =  {6, 8, 10, 12, 14, 16, 18}

and C = {x : x = 3n, n ∈ N and 4 ≤ n < 10}

C  =  {12, 15, 18, 21, 24, 27}

(B n C)  =  {12, 18}

 A−(B n C)  =   {0, 6, 24, 30}  ----(1)

(A − B)  =  {0, 24, 30}

(A − C)  =  {0, 6, 30}

 (A − B) U (A − C)  =  {0, 6, 24, 30}  ----(2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.