VERTEX FOCUS AND DIRECTRIX OF A PARABOLA

Symmetric about x-axis and opens to the right

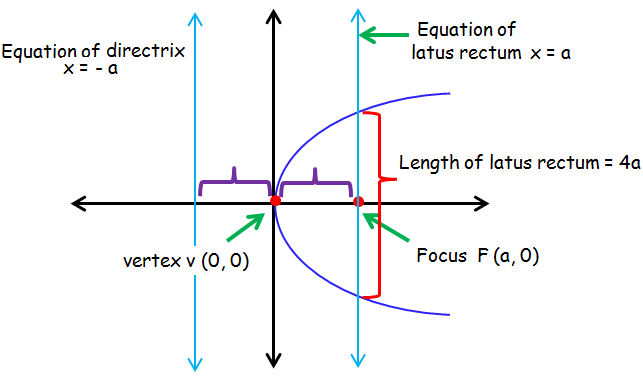
Equation of the parabola : y² = 4ax.

Axis of symmetry : x -axis.

Equation of axis of symmetry : y = 0.

Vertex V(0, 0).

Focus F(a, 0).

Equation of latus rectum : x = a.

Equation of directrix : x = -a.

Length of latus rectum : 4a.

Distance between directrix and latus rectum = 2a.

Symmetric about x-axis and opens to the left

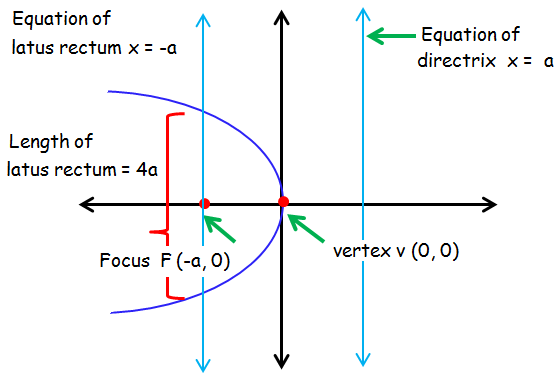
Equation of the parabola : y² = -4ax.

Axis of symmetry : x -axis.

Equation of axis of symmetry : y = 0.

Vertex V (0, 0).

Focus F (-a, 0).

Equation of latus rectum : x = -a.

Equation of directrix : x = a.

Length of latus rectum : 4a.

Distance between directrix and latus rectum = 2a.

Symmetric about y-axis and opens up

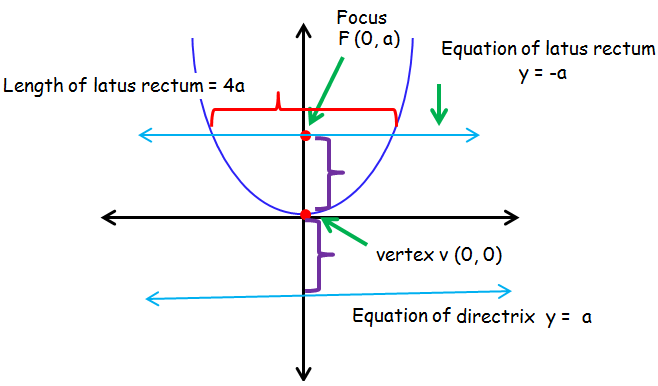
Equation of the parabola : x² = 4ay.

Axis of symmetry : y -axis.

Equation of axis of symmetry : x = 0.

Vertex V (0, 0).

Focus F (0, a).

Equation of latus rectum : y = a.

Equation of directrix : y = -a.

Length of latus rectum : 4a.

Distance between directrix and latus rectum = 2a.

Symmetric about y-axis and opens down

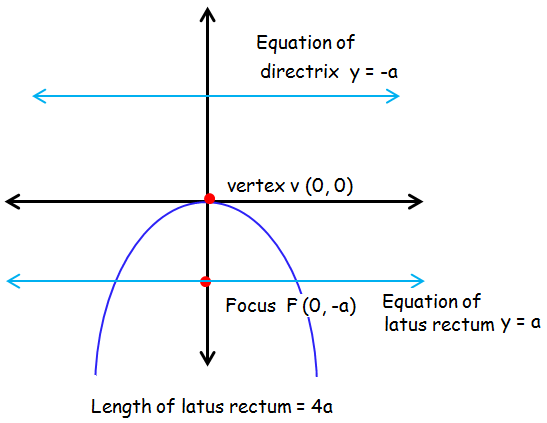
Equation of the parabola : x² = -4ay.

Axis of symmetry : y -axis.

Equation of axis : x = 0.

Vertex V (0, 0).

Focus F (0, -a).

Equation of latus rectum : y = -a.

Equation of directrix : y = a.

Length of latus rectum : 4a.

Distance between directrix and latus rectum = 2a.

In each of the following parabolas, find the vertex, axis of symmetry, focus, equation of the latus rectum, directrix and length of latus rectum.

Example 1 :

y² = 16x

Solution :

The given equation of parabola is in standard form. The parabola is symmetric about x-axis and it opens to the right.

4a = 16

a = 4

Vertex :

(0, 0)

Axis of symmetry :

x-axis or y = 0

Focus :

F(a, 0) = F(4, 0)

Equation of latus rectum :

x = a

x = 4

Equation of directrix :

x = -a

x = -4

Length of latus rectum :

= 4a

= 4(4)

= 16 units

Example 2 :

y = -4x²

Solution :

Write the given equation of parabola in standard form.

y = -4x²

y/(-4) = x²

x² = -y/4

x² = -(1/4)y

The  above equation of parabola is in standard form. The parabola is symmetric about y-axis and it opens down.

4a = 1/4

a = 1/16

Vertex :

(0, 0)

Axis of symmetry :

y-axis or x = 0

Focus :

F(0, -a) = F(0, -1/16)

Equation of latus rectum :

y = -a

y = -1/16

Equation of directrix :

y = a

y = 1/16

Length of latus rectum :

= 4a

= 4(1/16)

= 1/4 units

Example 3 :

(y + 2)² = -8(x + 1)

Solution :

(y + 2)² = -8(x + 1)

Let X = x + 1, Y = y + 2.

Y² = -8X

The  above equation of parabola is in standard form. The parabola is symmetric about X-axis and it opens to the left.

4a = 8

a = 2

Vertex :

(0, 0)

X = 0  and  Y = 0

x + 1 = 0  and  y + 2 = 0

x = -1  and  y = -2

The vertex is (-1, -2).

Axis of symmetry :

X-axis or Y = 0

y + 2 = 0

y = -2

The axis of symmetry is y = -2.

Focus :

F(-a, 0) = F(-2, 0)

x + 1 = -2  and  y + 2 = 0

x = -3  and  y = -2

The focus is (-3, -2).

Equation of latus rectum :

X = -a

X = -2

x + 1 = -2

x = -3

Equation of directrix :

X = a

X = 2

x + 1 = 2

x = 1

Length of latus rectum :

= 4a

= 4(2)

= 8 units

Example 4 :

x² - 2x + 8y + 17 = 0

Solution :

x² - 2x + 8y + 17 = 0

x² - 2(x)(1) + 1² - 1² = -8y - 17

(x - 1)² - 1² = -8y - 17

(x - 1)² - 1 = -8y - 17

(x - 1)² - 1 = -8y - 16

(x - 1)² = -8(y + 2)

Let X = x - 1 and Y = y + 2.

X² = -8Y

The  above equation of parabola is in standard form. The parabola is symmetric about Y-axis and it opens down.

4a = 8

a = 2

Vertex :

(0, 0)

X = 0  and  Y = 0

x - 1 = 0  and  y + 2 = 0

x = 1  and  y = -2

The vertex is (1, -2).

Axis of symmetry :

Y-axis or X = 0

x - 1 = 0

x = 1

The axis of symmetry is x = 1.

Focus :

F(0, -a) = F(0, -2)

x - 1 = 0  and  y + 2 = -2

x = 1  and  y = -4

The focus is (1, -4).

Equation of latus rectum :

Y = -a

Y = -2

y + 2 = -2

y = -4

Equation of directrix :

Y = a

Y = 2

y + 2 = 2

y = 0

Length of latus rectum :

= 4a

= 4(2)

= 8 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.