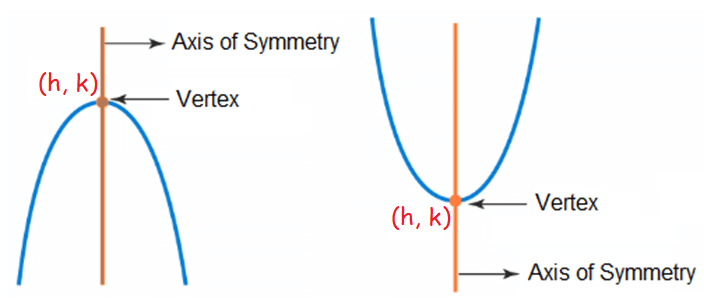
VERTEX FORM EQUATION OF A PARABOLA

When a parabola opens up/down, its vertex form equation is

y = a(x - h)² + k

where (h, k) is the vertex.

a < 0 ----> parabola opens down

a > 0 ----> parabola opens up

Write the following equations of the parabolas in vertex form :

Example 1 :

y = x² - 2x - 5

Solution :

y = x² - 2x - 5

y = x² - 2(x)(1) + 1² - 1² - 5

Using the identity (a - b)² = a² - 2ab + b²,

y = (x - 1)² - 1² - 5

y = (x - 1)² - 1 - 5

y = (x - 1)² - 6

Example 2 :

y = -x² - 14x - 59

Solution :

y = -x² - 14x - 59

y = -1(x² + 14x) - 59

y = -1[x² + 2(x)(7) + 7² - 7²] - 59

Using the identity (a + b)² = a² + 2ab + b²,

y = -1[(x + 7)² - 7²] - 59

y = -1[(x + 7)² - 49] - 59

y = -1(x + 7)² + 49 - 59

y = -1(x + 7)² - 10

Example 3 :

y = x² + 4x

Solution :

y = x² + 4x

y = x² + 2(x)(2) + 2² - 2²

Using the identity (a + b)² = a² + 2ab + b²,

y = (x + 2)² - 2²

y = (x + 2)² - 4

Example 4 :

y = 2(x - 5)(x - 3)

Solution :

y = 2(x - 5)(x - 3)

y = 2(x² - 3x - 5x + 15)

y = 2(x² - 8x + 15)

y = 2x² - 16x + 30

y = 2(x² - 8x) + 30

y = 2[x² - 2(x)(4)] + 30

y = 2[x² - 2(x)(4) + 4² - 4²) + 30

Using the identity (a + b)² = a² + 2ab + b²,

y = 2[(x - 4)² - 4²] + 30

y = 2[(x - 4)² - 16] + 30

y = 2[(x - 4)² - 32 + 30

y = 2(x - 4)² - 2

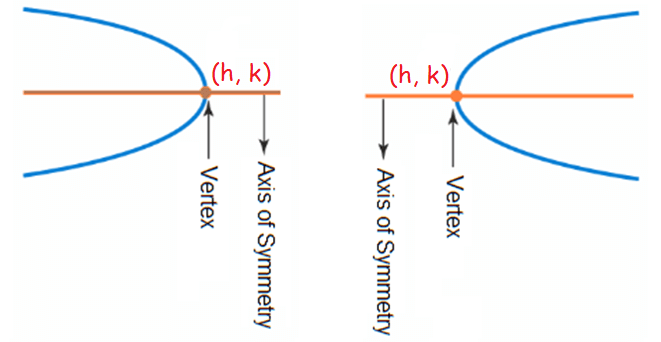
When a parabola opens to the left or right, its vertex form equation is

x = a(y - k)² + h

where (h, k) is the vertex.

a < 0 ----> parabola opens to the left

a > 0 ----> parabola opens up to the right

Write the following equations of the parabolas in vertex form :

Example 5 :

x = y² - 2y - 5

Solution :

x = y² - 2y - 5

x = y² - 2(y)(1) + 1² - 1² - 5

Using the identity (a - b)² = a² - 2ab + b²,

x = (y - 1)² - 1² - 5

x = (y - 1)² - 1 - 5

x = (y - 1)² - 6

Example 6 :

x = -y² - 14y - 59

Solution :

x = -y² - 14y - 59

x = -1(y² + 14y) - 59

x = -1[y² + 2(y)(7) + 7² - 7²] - 59

Using the identity (a + b)² = a² + 2ab + b²,

x = -1[(y + 7)² - 7²] - 59

x = -1[(y + 7)² - 49] - 59

x = -1(y + 7)² + 49 - 59

x = -1(y + 7)² - 10

Example 7 :

x = y² + 4y

Solution :

x = y² + 4y

x = y² + 2(y)(2) + 2² - 2²

Using the identity (a + b)² = a² + 2ab + b²,

x = (y + 2)² - 2²

x = (y + 2)² - 4

Example 8 :

x = -3(y - 2)(y + 8)

Solution :

x = -3(y - 2)(y + 8)

x = -3(y² + 8y - 2y - 16)

x = -3(y² + 6y - 16)

x = -3y² - 18y + 48

x = -3(y² + 6y) + 48

x = -3[y² + 2(y)(3)] + 48

x = -3[y² + 2(y)(3) + 3² - 3²] + 48

Using the identity (a + b)² = a² + 2ab + b²,

x = -3[(y + 3)² - 3²] + 48

x = -3[(y + 3)² - 9] + 48

x = -3(y + 3)² + 27 + 48

x = -3(y + 3)² + 75

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.