VERTEX FORM OF A QUADRATIC FUNCTION WORKSHEET

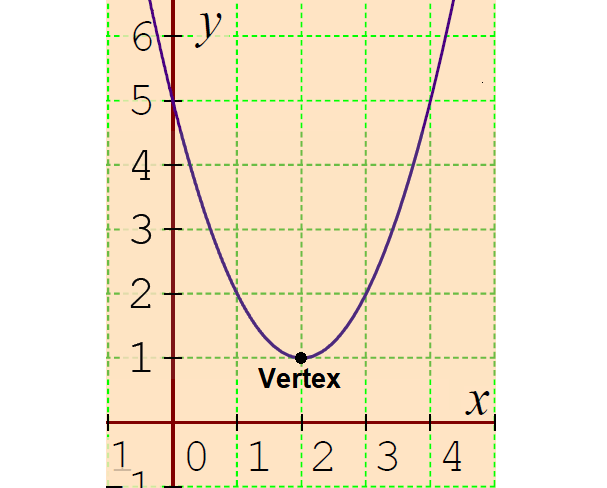
1. Write the quadratic function in vertex form whose graph is shown below.

Questions 2-4 : Write the quadratic function in vertex form and write its vertex.

2. f(x) = x² + 6x + 9

3. f(x) = -x² - 2x - 2

4. f(x) = 4x² + 16x + 5

5. Write the following quadratic function in vertex form and sketch its graph :

f(x) = -x² + 2x + 3

1. Answer :

The parabola above opens up with vertex (2, 1).

Vertex form of a quadratic function :

f(x) = a(x - h)² + k

Substitute vertex (h, k) = (2, 1).

f(x) = a(x - 2)² + 1 ----(1)

The y-intercept of the parabola is (0, 5). That is, the parabola is passing through (0, 5).

Substitute x = 0 and y = 5.

5 = a(0 - 2)² + 1

5 = a(- 2)² + 1

5 = 4a + 1

Subtract 1 from both sides.

4 = 4a

Divide both sides by 4.

1 = a

Substitute a = 1 in (1).

f(x) = 1(x - 2)² + 1

2. Answer :

Vertex form of the quadratic function :

f(x) = x² + 6x + 9

f(x) = x² + 2(x)(3) + 3²

f(x) = (x + 3)²

Vertex :

Comparing y = a(x - h)² + k and f(x) = (x + 3)²,

h = -3 and k = 0

So, the vertex is (h, k) = (-3, 0).

3. Answer :

Vertex form of the quadratic function :

f(x) = -x² - 2x - 2

f(x) = -(x² + 2x) - 2

f(x) = -[x² + 2(x)(1) + 1² - 1²] - 2

f(x) = -[(x + 1)² - 1²] - 2

f(x) = -[(x + 1)² - 1] - 2

f(x) = -(x + 1)² + 1 - 2

f(x) = -(x + 1)² - 1

Vertex :

Comparing f(x) = a(x - h)² + k and f(x) = -(x + 1)² - 1,

h = -1 and k = -1

So, the vertex is (h, k) = (-1, -1).

4. Answer :

Vertex form of the quadratic function :

f(x) = 4x² + 16x + 5

f(x) = 4(x² + 4x) + 5

f(x) = 4[x² + 2(x)(2) + 2² - 2²] + 5

f(x) = 4[(x + 2)² - 2²] + 5

f(x) = 4[(x + 2)² - 4] + 5

f(x) = 4(x + 2)² - 16 + 5 

f(x) = 4(x + 2)² - 11

Vertex :

Comparing f(x) = a(x - h)² + k and f(x) = 4(x + 2)² - 11,

h = -2 and k = -11

So, the vertex is (h, k) = (-2, -11).

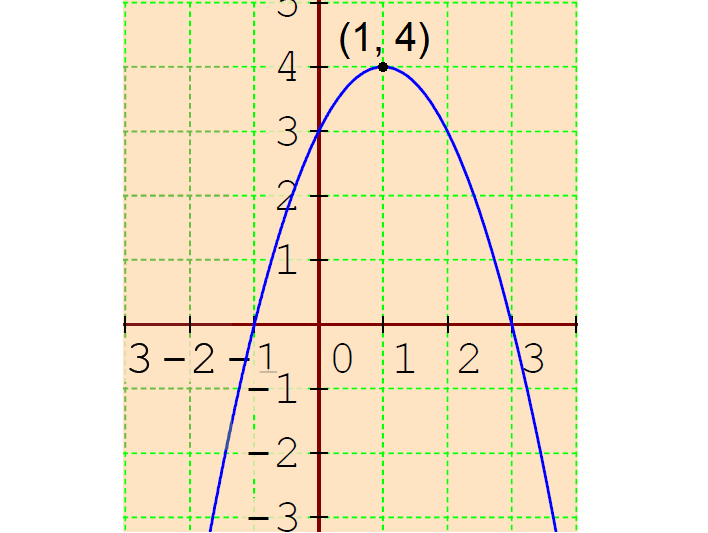
5. Answer :

Vertex form of the quadratic equation :

f(x) = -x² + 2x + 3

f(x) = -(x² - 2x) + 3

f(x) = -[x² - 2(x)(1) + 1² - 1²] + 3

f(x) = -[(x - 1)² - 1²] + 3

f(x) = -[(x - 1)² - 1] + 3

f(x) = -(x - 1)² + 1 + 3

f(x) = -(x - 1)² + 4

Vertex :

Comparing f(x) = a(x - h)² + k and f(x) = -(x - 1)² + 4,

h = 1 and k = 4

So, the vertex is (h, k) = (1, 4).

To graph the above quadratic equation, we need to find x-intercept and y-intercept, if any.

x-intercept :

To find the x-intercept, substitute f(x) = 0.

0 = -(x - 1)² + 4

(x - 1)² = 4

Take square root on both sides.

x - 1 = ±√4

x - 1 = ±2

x - 1 = -2  or  x - 1 = 2

x = -1  or  x = 3

So, the x-intercepts are (-1, 0) and (3, 0) .

y-intercept :

To find the y-intercept, substitute x = 0.

f(0) = -(0 - 1)² + 4

= -(-1)² + 4

= -1 + 4

= 3

y = 3

So, the y-intercept is (0, 3).

Comparing f(x) = a(x - h)² + k and f(x) = -(x - 1)² + 4,

a = -1

So, the parabola opens down with vertex (1, 4), x-intercepts (-1, 0) and (3, 0) and y-intercept (0, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.