VERTICES OF RECTANGLE WORKSHEET

Problem :

Examine whether the given points  A (-3,2) and B (4,2) and C (4,-3) and D (-3,-3) forms a rectangle.

Solution :

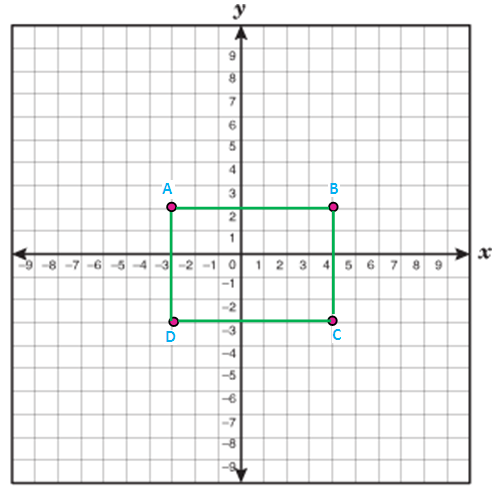
Solution :

To show that the given points forms a rectangle, we need to find the distance between given points.

Distance Between Two Points (x ₁, y₁) and (x₂ , y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Four points are A (-3,2) and B (4,2) and C (4,-3) and D (-3,-3)

Distance between the points A and B

= √(x₂ - x₁)² + (y₂ - y₁)²

Here x₁ = -3, y₁ = 2, x₂ = 4  and  y₂ = 2

=    √(4-(-3))² + (2-2)²

=    √(4+3)² + (0)²

=    √7² + 0

=    √49

=     7 units

Distance between the points B and C

 =  √(x₂ - x₁)² + (y₂ - y₁)²

Here x₁ = 4, y₁ = 2, x₂ = 4  and  y₂ = -3

=    √(4-4)² + (-3-2)²

=    √(0)² + (-5)²

=    √0 + 25

=    √25

=    5 units

Distance between the points C and D

= √(x₂ - x₁)² + (y₂ - y₁)²

Here x₁ = 4, y₁ = -3, x₂ = -3  and  y₂ = -3

=    √(-3-4)² + (-3-(-3))²

=    √(-7)² + (-3+3)²

=    √49 + 0

=    √49

=     7 units

Distance between the points D and A

= √(x₂ - x₁)² + (y₂ - y₁)²

Here x₁ = -3, y₁ = 2, x₂ = -3  and  y₂ = 2

=    √(-3-(-3))² + (2-(-3))²

=    √(-3+3)² + (2+3)²

=    √0 + 5²

=    √25

=    5 units

AB = 7 units

BC = 5 units

CD = 7 units

DA = 5 units

Length of opposite sides are equal.To test whether it forms right triangle we need to find the length of diagonal AC.

Distance between the points A and C

= √(x₂ - x₁)² + (y₂ - y₁)²

Here x₁ = -3, y₁ = 2, x₂ = 4  and  y₂ = -3

=    √(4-(-3))² + (-3-2)²

=    √(4+3)² + (-5)²

=    √7² + 5²

=    √49 + 25

=    √74

=    √74 units

AC² = AB² + BC²

√74² = 7² + 5²

74 = 49 + 25

74 = 74

So the given vertices forms a rectangle.  

Try other questions

(1)  Examine whether the given points  A (-3,2) and B (4,2) and C (4,-3) and D (-3,-3) forms a rectangle.

(2)  Examine whether the given points  A (8,3) and B (0,-1) and C (-2,3) and D (6,7) forms a rectangle.

(3)  Examine whether the given points  A (-2,7) and B (5,4) and C (-1,-10) and D (-8,-7) forms a rectangle.

(4)  Examine whether the given points  P (-3,0) and Q (1,-2) and R (5,6) and S (1,8) forms a rectangle.

(5)  Examine whether the given points  P (-1,1) and Q (0,0) and R (3,3) and S (2,4) forms a rectangle.

(6)  Examine whether the given points  P (5,4) and Q (7,4) and R (7,-3) and S (5,-3) forms a rectangle.

(7)  Examine whether the given points  P (0,-1) and Q (-2,3) and R (6,7) and S (8,3) forms a rectangle.

(8)  Examine whether the given points  A (2,-2) and B (8,4) and C (5,7) and D (-1,1) forms a rectangle.

Related topics

• Solution for vertices of rectangle question1
• Solution for vertices of rectangle question2
• Solution for vertices of rectangle question3
• Solution for vertices of rectangle question4
• Solution for vertices of rectangle question5
• Solution for vertices of rectangle question6
• Solution for vertices of rectangle question7
• Solution for vertices of rectangle question8

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.