VOLUME OF 3D SHAPES EXAMPLES

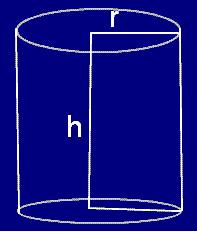
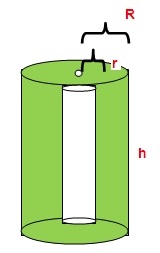
Volume  =  Πr2h	Volume  =  Πh(R2 - r2)
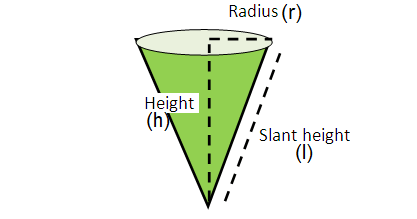
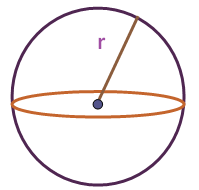
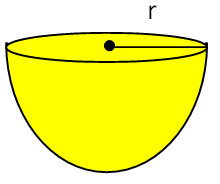
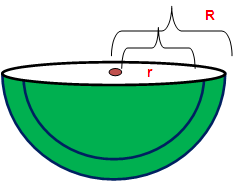
Volume  =  (1/3) Πr2h	Volume  =  (4/3) Πr3 Volume of hollow sphere   =  (4/3) Π(R3 - r3)
Volume  =  (2/3) Πr3	Volume = (2/3)Π(R3 - r3)
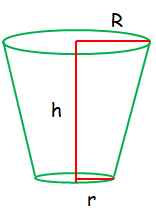	Volume = (1/3)Πh(R2 + r2 + Rr)

Example 1 :

A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.

Solution :

Given radius of the well = 5 m

Height of the well = 14 m

Width of the embankment = 5 m

Radius of the embankment = 5 + 5 = 10 m

Let h be the height of the embankment

Hence the volume of the embankment = volume of the well 

That is,  π(R² – r²)h = πr²h

 (10² – 5²)h = 5²(14)

(100 - 25)h  =  25(14)

h  =  25(14)/75

h  =  14/3

h = 4.67 m

Hence the height of the embankment is 4.67 m.

Example 2 :

A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?

Solution :

Measurement of glass :

Radius of glass  =  10 cm

height of glass  =  h

Measurement of small metal :

Radius of metal  =  5 cm

height of glass  =  4 cm

The quantity of water raised in the cylindrical glass  =  volume of small cylindrical metal

 πr²h  =   πr²h

 10² h  =  5² (4)

  h  =  100/100

  h  =  1 cm

Example 3 :

If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.

Solution :

Circumference of piece  =  484 cm

2 π r  =  484

2 (22/7) r  =  484

r  =  484 (7/22) (1/2)

  r  =  77

Volume of cone  =  (1/3) πr²h

=  (1/3)⋅ (22/7) ⋅ 77² ⋅ (105)

=  652190 cm³

Example 4 :

A conical container is fully filled with petrol. The radius is 10m and the height is 15 m. If the container can release the petrol through its bottom at the rate of 25 cu.meter per minute, in how many minutes the container will be emptied. Round off your answer to the nearest minute.

Solution :

Volume of petrol in the container  =  (1/3) πr²h

Radius  =  10 m, height  =  15 m

Releasing rate  =  25 cu.meter

Number of minutes  =  (1/3) π10²(15) / 25

  =  (1/3) (22/7) 10²(15) / 25

  =  62.85

  =  63 minutes

Example 4 :

Volume of a cylinder is 324 π yd³. The height of the cylinder is 16 yd. What is the radius of the cylinder ?

Solution :

Volume of a cylinder = 324 π yd³

πr²h = 324 π

r²h = 324

height = 16 yd

r²(16) = 324

r² = 324/16

r² = 20.25

r = 4.5 yd

So, the radius of the cylinder is 4.5 yd.

Example 5 :

A cone has a volume of 2544 cubic centimeters and the diameter of 18 cm, what is the height of cone ?

Solution :

Volume of petrol in the container  =  (1/3) πr²h

 (1/3) πr²h = 2544

Diameter = 18 cm

radius = 9 cm

 (1/3) π(9)²h = 2544

h = 2544 x (3) / (81 x 3.14)

h = 30 cm

So, the required height of the cone is 30 cm.

Example 6 :

A right rectangular prism has a volume of 440 in³. The length and width of the prism is 8 in by 11 inches. What is the height of the prism ?

Solution :

Volume of rectangular prism = 440 in³

length x width x height = 440

length = 8 inches, width = 11 inches, height = ?

8 x 11 x height = 440

height = 440 / (8 x 11)

= 5 inches

So, the height of the rectangular prism is 5 inches.

Example 7 :

The diameter of the hemispherical dome is 28 inches. What is the volume. Leave your answer in π.

Solution :

Diameter = 28 inches

radius = 14 inches

Volume of hemisphere = (2/3) πr³

= (2/3) x π x (14)³

= 5488/3 π cubic inches.

= 1829.3 π cubic inches

So, the required volume of the dome is 1829.3 π cubic inches.

Example 8 :

A shaved ice vender wants a new cone to hold about 150 cm³ of shaved ice when filled to the brim. If the height of the cone is p cm, what should be the radius of the cone ?

Solution :

Capacity of the cone = 150 cm³

height of the cone = 9 

Volume of cone = (1/3) πr² h

 (1/3) πr² h = 150

 (1/3) x (22/7)r² 9 = 150

r² = 150 x (7/22) x 3 x (1/9)

r² = 15.9

r = 3.9 

Approximately 4 cm.

So, the radius of the cone is 4 cm.

Example 9 :

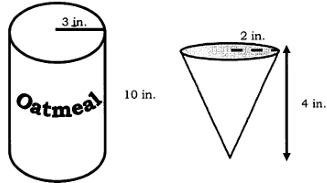
Ms. Clays wants to fill her oatmeal container in the shape of cylinder full of oatmeal. She has a cone shape scoop that she will use to fill the container. How many scoops will it take Ms. Clays to fill the entire cylinder of oatmeal ? 

Solution :

Let n be the number of scoops.

n x volume of cone container = volume of cylindrical container

n x (1/3) πr² h = πr² h

Radius of cylinder = 3 inches

height of cylinder = 10 inches

radius of cone = 2 inches

height of cone = 4 inches

n x (1/3) π(2)² x 4 = π(3)² (10)

n x (1/3) (2)² x 4 = (3)² (10)

n = (9 x 10 x 3) / 16

n = 16.875

Approximately 17 scoops.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.