VOLUME OF CYLINDER QUESTIONS AND ANSWERS

Question 1 :

Volume of a solid cylinder is 62.37 cu.cm. Find the radius if its height is 4.5 cm

Solution :

Height of solid cylinder  =  4.5 cm

Volume of cylinder  =  62.37 cu.cm

πr²h  =  62.37

 (22/7) ⋅ r²⋅4.5  =  62.37

r²  =  62.37 ⋅ (1/4.5) ⋅ (7/22)

r²  =  13.86 ⋅ (7/22)

r²  =  97.02/22

r²  =  4.41

r  =  √(2.1 ⋅ 2.1)

r  =  2.1 cm

Radius of the cylinder  =  2.1 cm

Question 2 :

The radii of two right circular cylinders are in the ratio 2:3. Find the ratio of their volumes if their heights are in the ratio 5:3.

Solution :

Let r₁ and r₂ are the radii of two cylinders.

Let h₁ and h₂ are the heights of two cylinders.

r₁ : r₂  =  2:3

r₁/r₂  =  2/3

r₁  =  2r₂/3

h₁ : h₂  =  5 : 3

h₁/h₂  =  5/3

h₁  =  5h₂/3

Volume of cylinder  =  πr²h

πr₁²h₁ : πr₂² h₂

(2r₂/3)² (5h₂/3) : r₂² h₂

 (4 r₂²/9)(5h₂/3) : r₂² h₂

20/27 : 1

20 : 27

Ratio of volume of two cylinders 20 : 27

Question 3 : 

The radius and height of two circular cylinders are in the ratio 5 : 7. If its volume is 4400 cu.cm, find the radius of the cylinder.

Solution :

Let r and h are the radius and height of cylinder

r : h  =  5 : 7

r/h  =  5/7

r  =  5h/7

Volume of the cylinder  =  4400 cu.cm

πr²h  =  4400

(22/7) (5h/7)² ⋅ h = 4400

(22/7) ⋅ (25h²/49) ⋅ h  =  4400

h³ = 4400 ⋅ (7/22) ⋅ (49/25)

h³  =  176 ⋅ (7/22) ⋅ 49

h³  =  8 ⋅ 7 ⋅ 7 ⋅ 7

h  =  14 cm

r  =  5(14)/7

r  =  10 cm

Radius of the cylinder = 10 cm.

Question 4 :

A rectangular sheet of metal foil with dimension 66 cm x 12 cm is rolled to form a cylinder of height 12 cm. Find the volume of the cylinder.

Solution :

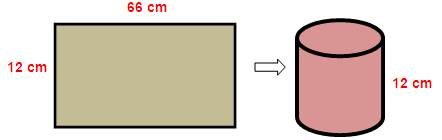
Length of metal sheet  =  66 cm

Width of sheet = 12 cm

Circumference of the base of the cylinder  =  66 cm

2πr  =  66

2 ⋅ (22/7) ⋅ r  =  66

r  =  66 ⋅ (1/2) ⋅ (7/22) 

r  =  3 ⋅ (1/2) ⋅ 7

r  =  21/2

r  =  10.5 cm

Volume of the right circular cylinder  =  πr²h

=  (22/7) ⋅ (10.5)² ⋅ 12

=  (22/7) ⋅ 10.5 ⋅ 10.5 ⋅ 12

=  4158 cm³

Volume of the the right circular cylinder = 4158 cm³

Question 5 :

A lead pencil is in the shape of right circular cylinder. The pencil is 28 cm long and its radius is 3 mm. If the lead is of radius 1 mm, then find the volume of the wood used in the pencil.

Solution :

Height of the pencil = 28 cm

Outer radius (R)  =  3 mm

Inner radius (r)  =  1 mm

Now we have to change the units from mm to cm. For that we have to divide it by 10.

R  =  3/10  =  0.3 cm

r  =  1/10

r  = 0.1 cm

To find the volume of the wood used to make that pencil, simply we can find the volume of the pencil. Pencil is in the shape of hollow cylinder

Volume of hollow cylinder  =  πh(R²-r²)

=   (22/7) ⋅ 28 ⋅ (0.3²-0.1²)

=  22 ⋅ 4 ⋅ (0.09-0.01)

=  7.04 cm³

Volume of wood used in the pencil  =  7.04 cm³.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.