VOLUME OF PRISM

Prism is basically a 3D shape. Even though we have different formulas to find volume of different kinds of prisms, the basic idea of finding volume is to multiply the base area and height of the prism.

When we are trying to find volume of a prism, we have to consider the following cases. 

Case 1 :

Let the base of a prism be a rectangle or square. If all the side walls are either rectangles or squares (that is, no side wall is triangle), then prism will look like as given below. 

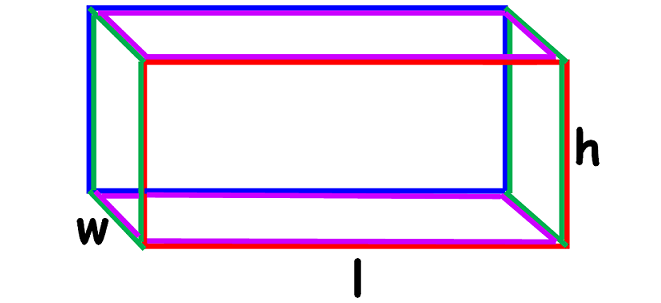
The formula to find volume of the above prism 

= Base Area x Height

Case 2 :

Let the base of a prism be a rectangle or square. If two of the side walls side walls are triangles and other two side walls are rectangles or squares, then prism will look like as given below. 

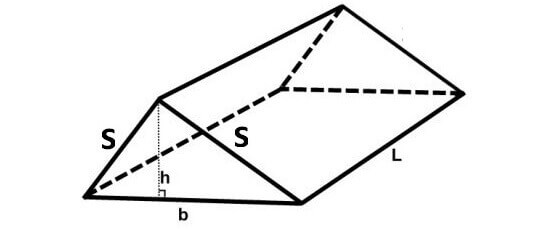
The formula to find volume of the above prism 

= (1/2) x Base Area x Height

Case 3 :

Let the base of a prism be a triangle. If all of the side walls are rectangles or squares, then the prism will look like as given below.  

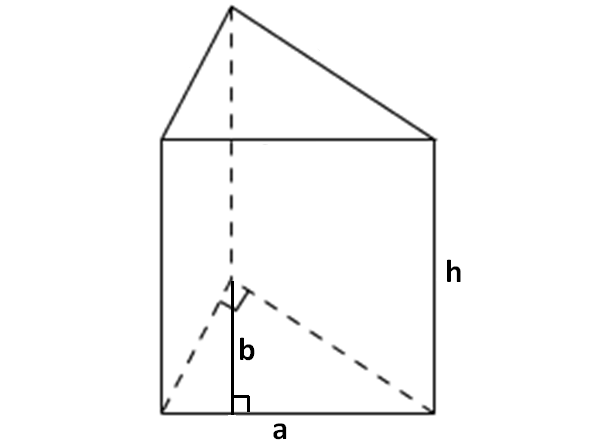
The formula to find volume of the above prism 

= Base Area x Height

Case 4 :

Let the base of a prism be a rectangle or square or triangle. If all of the side walls are triangles, then the prism will be a pyramid and it will look like as given below. 

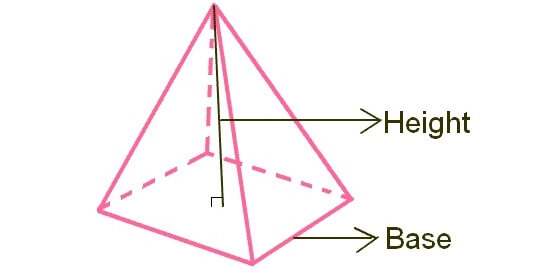
The formula to find volume of the above pyramid 

= (1/3) x Base area x Height

Example 1 :

Find the volume of the cuboid shown below.

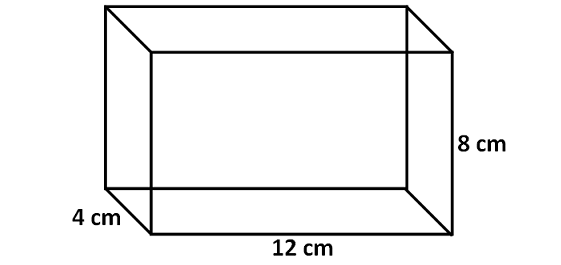
Solution :

Here, the base is  a rectangle and all the side walls are also rectangles.

Then, formula for volume of the above cuboid is

= Base Area x Height

Here, the base is a rectangle with length 12 cm and width 4 cm.

Area of base is

= 12 x 4 = 48 cm²

Height of the cuboid is 8 cm.

So, volume of the above cuboid is

= 48 x 8

= 384 cm³

Example 2 :

Find the volume of the cube shown below.

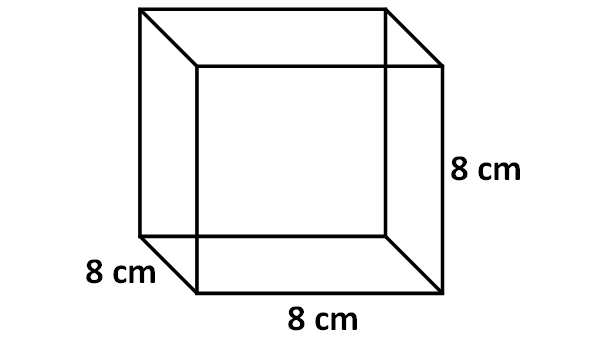
Solution :

Here, the base is  a square and all the side walls are also squares.

Then, formula for volume of the above cube is

= Base area x Height

Here, the base is a square with side length of 8 cm.

Area of base is

= 8 x 8

= 64 cm²

Height of the cube is 8 cm.

So, volume of the above cube is

= 64 x 8

= 512 cm³

Example 3 :

Find the volume of the triangular prism given below.

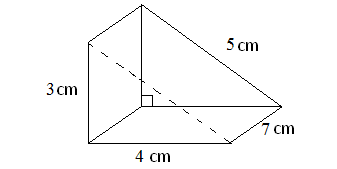
Solution :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, formula for the above triangular prism is

= (1/2) x Base area x Height

Here, the base is a rectangle with length 7 cm and width is 4 cm.

So, area of the base is

= 7 x 4

= 28  cm²

Height of the prism is 3 cm.

So, volume of the above triangular prism is

= (1/2) x 28 x 3

= 42 cm³

Example 4 :

Find the volume of the triangular prism shown below.

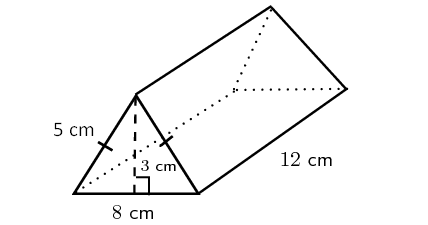
Solution :

Here, the base is  a rectangle, two of the side walls are triangles and other two side walls are rectangles.

Then, formula for the above triangular prism is

= (1/2) x Base area x Height

Here, the base is a rectangle with length 12 cm and width is 8 cm.

So, area of the base is

= 12 x 8

= 96 cm²

Height of the prism is 3 cm.

So, volume of the above triangular prism is

= (1/2) x 96 x 3

= 144 cm³

Example 5 :

Find the volume of the triangular prism shown below.

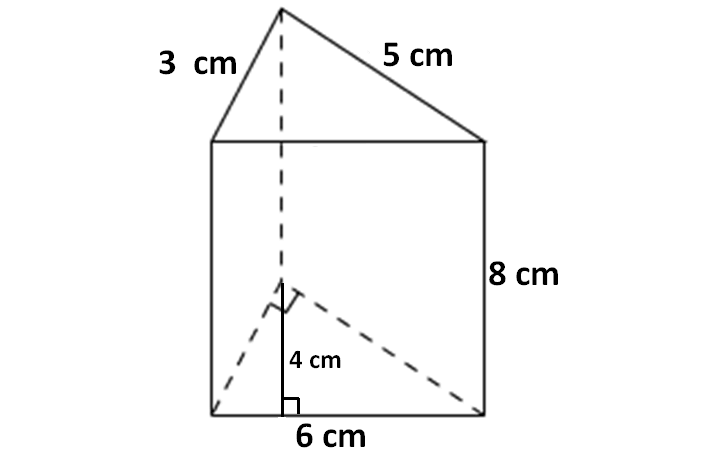
Solution :

Here, the base is  a triangle, and all the side walls are rectangles.

Then, formula for the above triangular prism is

= Base area x Height

Here, the base is a triangle with base 6 cm and height 4 cm.

So, area of the base is

= (1/2) x 6 x 4

= 12 cm²

Height of the prism is 8 cm.

So, volume of the above triangular prism is

= 12 x 8

= 96 cm³

Example 6 :

Find the volume of the pyramid shown below.

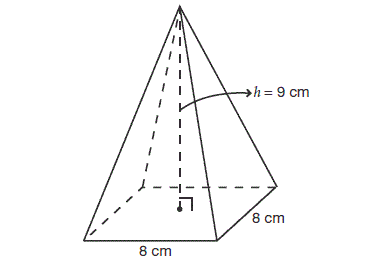
Solution :

Here, the base is  a square, and all the side walls are triangles.

Then, formula for the above triangular prism is

= (1/3) x Base area x Height

Here, the base is a square with side length 8 cm.

So, area of the base is

= 8 x 8

= 64 cm²

Height of the pyramid is 9 cm.

So, volume of the above triangular prism is

= (1/3) x 64 x 9

= 192 cm³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.