VOLUME OF UNIFORM CROSS SECTION WORKSHEET

Problem 1 :

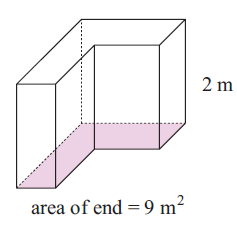
Problem 2 :

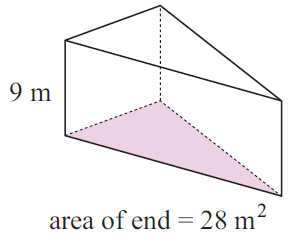
Problem 3 :

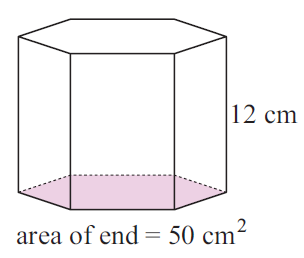
Problem 4 :

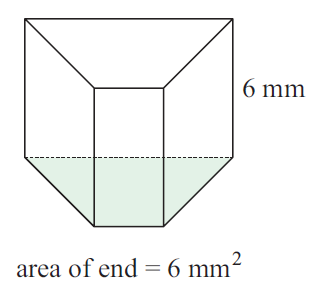
Problem 5 :

Problem 6 :

Problem 7 :

An empty garage has floor area 80 m² and a roof height of 4 m. Find the volume of air in the garage.

Problem 8 :

Each month a rectangular swimming pool 6 m by 5 m by 2 m deep costs $0.50 per cubic meter of water to maintain. How much will it cost to maintain the pool for one year?

Problem 9 :

Concrete costs $128 per cubic meter. What will it cost to concrete a driveway 20 m long and 3 m wide to a depth of 12 cm?

Problem 10 :

64 cartons of paper are delivered to your school. Each carton measures 40 cm by 30 cm by 25 cm. Is it possible to fit all the cartons into a storage cupboard 1 m by 1 m by 2 m? Explain your reasoning, using a diagram if you wish.

Problem 11 :

The breadth of the room is twice its height and is half of its length. The volume of room is 512 cm³, then its dimensions are

Problem 1 :

Solution :

Given :

Area of end  =  9 m²

Height of the solid  =  2 m

Volume  =  9 (2)

=  18 m³

Problem 2 :

Solution :

Given :

Area of end  =  28 m²

Height of the solid  =  9 m

Volume  =  28 (9)

=  252 m³

Problem 3 :

Solution :

Given :

Area of end  =  50 cm²

Height of the solid  =  12 cm

Volume  =  50 (12)

=  600 cm³

Problem 4 :

Solution :

Given :

Area of end  =  6 mm²

Height of the solid  =  6 mm

Volume  =  6(6)

=  36 mm³

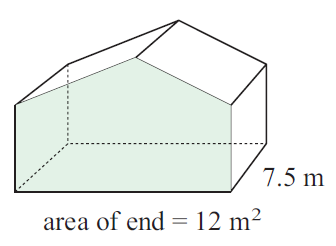
Problem 5 :

Solution :

Given :

Area of end  =  12 m²

Height of the solid  =  7.5 m

Volume  =  12(7.5)

=  90 m³

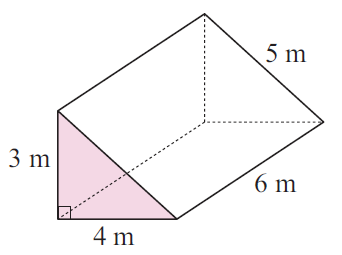
Problem 6 :

Solution :

Area of base triangle  =  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ 4 ⋅ 3

=  6 m²

Height  =  6 m

Volume  =  Base area x height

=  6 (6)

=  36 m³

Problem 7 :

An empty garage has floor area 80 m² and a roof height of 4 m. Find the volume of air in the garage

Solution :

Area of base  =  80 m²

height  =  4 m

Volume  =  Area of base x height

=  80 (4)

=  320 m³

Problem 8 :

Each month a rectangular swimming pool 6 m by 5 m by 2 m deep costs $0.50 per cubic meter of water to maintain. How much will it cost to maintain the pool for one year?

Solution :

Volume of rectangular swimming pool 

=  Base area x height

Area of rectangular base with length 6 m and width = 5 m.

=  6(5)

=  30 m²

Height  =  2 m

Volume  =  30(2)

=  60 m³

Cost of maintaining  =  0.50 per cubic meter

=  60 (0.50)

=  $30 (per month)

Cost of maintaining per year  =  =  30(12)

=  $360

Problem 9 :

Concrete costs $128 per cubic meter. What will it cost to concrete a driveway 20 m long and 3 m wide to a depth of 12 cm?

Solution :

Cost of concrete  =  $128 per cubic meter

length  =  20 m, width  =  3 m and height  =  0.12 m

Volume of concrete  =  20 x 3 x 0.12

=  7.2

Required cost  =  7.2(128)

=  $921.6

Problem 10 :

64 cartons of paper are delivered to your school. Each carton measures 40 cm by 30 cm by 25 cm. Is it possible to fit all the cartons into a storage cupboard 1 m by 1 m by 2 m? Explain your reasoning, using a diagram if you wish.

Solution :

length  =  40 cm  ==>  0.40 m

width  =  30 cm ==>  0.30 m

and height  =  25 cm  ==>  0.25 m

Volume of 1 carton  =  0.40 x 0.30 x 0.25

=  0.03 m³

Volume of 64 cartons  =  64(0.03)

=  1.92 m³

Volume of cupboard  =  1 x 1 x 2

=  2 m³

So, it is not possible to fit all in the cupboard.

Problem 11 :

The breadth of the room is twice its height and is half of its length. The volume of room is 512 cm³, then its dimensions are

Solution :

Let l, b and h be length, breadth and height of the rectangular prism.

b = 2h = l/2

deriving the measures for the same variable b,

l/2 = b

l = 2b, 2h = b, then h = b/2

volume of the rectangular prism

= length x breadth x height

2b (b)(b/2) = 512

b³ = 512

b³ = 8³

b = 7 cm

l = 2b ==> l = 2(7) = 14 cm

h = b/2 ==> 7/2 = 3.5 cm

So, the measures are 14 cm, 7 cm and 3.5 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.