VOLUME WITH CROSS SECTION PERPENDICULAR TO X AXIS

We can use definite integrals to find volume of a solid with specific cross sections on the interval.

For example, cross section may be any one of the shapes given below.

Squares, rectangles, semicircles, triangles etc.

If the cross section is perpendicular to x-axis and its  area is a function of x, say A(x), then the volume V of the solid on [a, b] can be found using the formula 

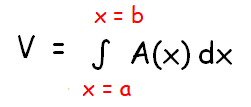
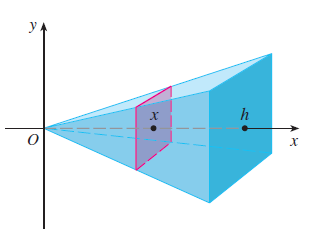
If the cross section is perpendicular to y-axis and its  area is a function of y, say A(y), then the volume V of the solid on [a, b] can be found using the formula 

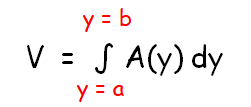
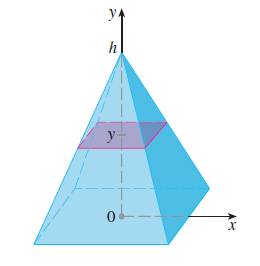
Example 1 :

Find the volume of the solid whose base is bounded by the circle

x² + y² = 4

the cross sections perpendicular to the x-axis are squares.

Solution :

Since the cross sections are perpendicular to x axis, we should express the area in terms of x.

Deriving the value of y from the given equation, we get

y²  =  4-x²

y  =   √4-x²

The cross sections are squares. So, A(x)  =  Area of square.

Area of square  =  a²

(Where a is a side length of square).

Note :

Cross sections are perpendicular to x axis, so to find length of square, we derive the given equation in terms of x.

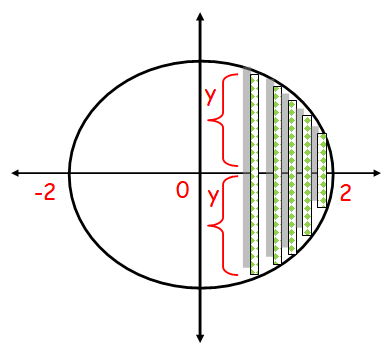
Side length of square  =  2y

2y  =   2√(4-x²)

Area of square :

A(x)  =  (2y)²  ==>   (2√(4-x²))²

A(x)  =  4(4-x²) 

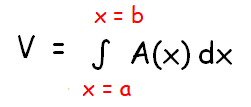
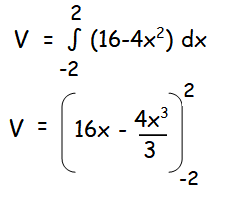
=  32 - (32/3) - (-32+(32/3))

=  32 - (32/3) + 32-(32/3)

=  64 - 64/3

=  (192-64)/3

=  128/3

Example 2 :

The base of S is the region enclosed by

y = 2-x²

and the x-axis. Cross-sections perpendicular to the y-axis are quarter-circles.

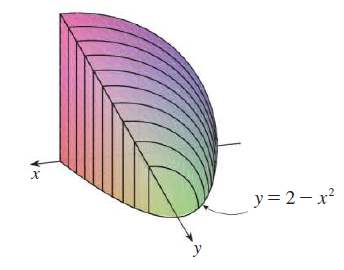
Solution :

Cross sections are perpendicular to y axis and we have to derive the given function in terms of x.

y = 2-x²

x²  =  2-y

x  =  √(2 - y)

2x  =  2√(2 - y)

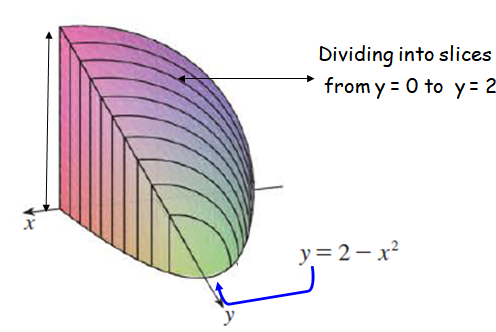
Radius of quarter circle  =  r  =  2x

Area of quarter circle  =  (1/4) πr²

A(y)  =  (1/4) π(2√(2 - y))²

A(y)  =  π(2 - y)

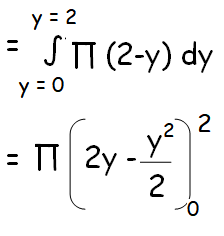
=  π [4-(4/2)]

=  2π

Example 3 :

For each problem, find the volume of the specified solid. The base of a solid is the region enclosed by y = 1 and y = x². Cross-sections perpendicular to the y-axis are squares

Solution :

Cross sections are perpendicular to y axis and we have to derive the given function in terms of x.

y = x²

x = √y

Side length = √y + √y

= 2√y

Area of square :

A(x) = (2√y)²

= 4y

= Integral 0 to 1 (4y) dy

= (4y²/2)

Applying the limits, we get

= 2y²

= 2(1)² - 2(0²)

= 2

So, the required volume is 2 cubic units.

Example 4 :

For each problem, find the volume of the specified solid. The base of a solid is the region enclosed by y = 1 and y = x². Cross-sections perpendicular to the y-axis are squares

Solution :

Cross sections are pe

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.