WHAT ARE UNLIKE FRACTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Unlike fractions are the fractions that have different denominators.
Example :
The picture below practically illustrates unlike fractions.
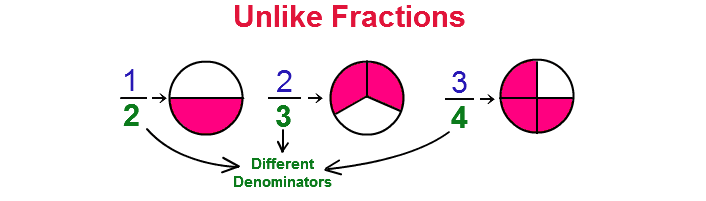
Adding and Subtracting Unlike Fractions
The following steps would be useful to add/subtract unlike fractions.
Step 1 :
Find the least common multiple of the denominators either by prime factorization or division method.
Step 2 :
Using multiplication, make each denominator as the value of the least common multiple found in step 2.
Step 3 :
At the end of step 2, you will have the same denominator. Take the denominator once and add/subtract the numerators.
Example 1 :
Evaluate :
Solution :
The above two fractions have different denominators. So, they are unlike fractions.
To add the above two fractions, we have to get the same denominator using the least common multiple of the denominators 4 and 6.
Find the least common multiple of 4 and 6 by prime factorization :
Resolve the given numbers into their prime factors.
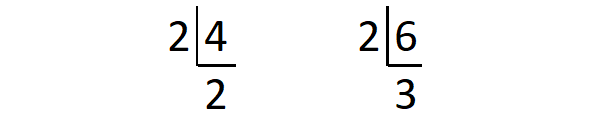
From the above division,
4 = 2 x 2
6 = 2 x 3
The different prime factors are 2 and 3.
The prime factor 2 appears a maximum of 2 times in the prime factorization of 4.
The prime factor 3 appears a maximum of 1 time in the prime factorization of 6.
Therefore, the least common multiple of 4 and 6 is
= 2 x 2 x 3
= 12
Using multiplication, make each denominator as 12 and add the two fractions.
Example 2 :
Evaluate :
Solution :
The above two fractions have different denominators. So, they are unlike fractions.
To add the above two fractions, we have to get the same denominator using the least common multiple of the denominators 12 and 18.
Find the least common multiple of 12 and 18 by division method :
Using L division, divide both the numbers by a common divisor. Continue this process, until you get a common divisor for both the numbers.
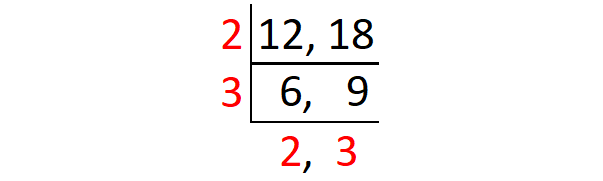
The least common multiple of 12 and 18 is
= 2 x 3 x 2 x 3
= 36
Using multiplication, make each denominator as 36 and subtract the two fractions.
Example 3 :
Evaluate :
Solution :
The above fractions have different denominators. So, they are unlike fractions.
To add the above two fractions, we have to get the same denominator using the least common multiple of the denominators 4, 6, 8 and 12.
Find the least common multiple of 4, 6, 8 and 12 by division method :
Using L division, divide the given numbers by a common divisor. Continue this process, until you get a common divisor at least for any of the two numbers.

The least common multiple of 4, 6, 8 and 12 is
= 2 x 2 x 3 x 1 x 1 x 2 x 1
= 24
Using multiplication, make each denominator as 24 and evaluate the given expression.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

