WORD PROBLEMS BASED ON DIVISION ALGORITHM

Problem 1 :

Find all positive integers, when divided by 3 leaves remainder 2.

Solution :

By using the division algorithm, we may easily get the answer

a = bq + r

To get the 1^st number, let q = 0, r = 2 (given) and b = 3 (given)

a = 3(0) + 2

a  = 2

To get the 2^nd number, let q = 1, r = 2 (given) and b = 3 (given)

a = 3(1) + 2

a  = 5

To get the 3^rd number, let q = 2, r = 2 (given) and b = 3 (given)

a = 3(2) + 2

a  = 8

The next number will be 3 more than the preceding number.

2, 5, 8, 11, 14, ............

Problem 2 :

A man has 532 flower pots. He wants to arrange them in rows such that each row contains 21 flower pots. Find the number of completed rows and how many flower pots are left over.

Solution :

Total number of flower pots  =  532

Number of flower pots in each row  =  21

Now, we have to find how many groups of 21 in 532. So, we use the concept division.

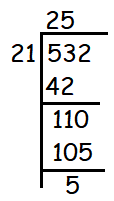
We may arrange the flower pots in 25 rows with each row consists of 21 pots.

The remaining number of flower pots  =  5.

Problem 3 :

Prove that the product of two consecutive positive integers is divisible by 2.

Solution :

Let "x" be the positive integer, the consecutive number be "x + 1"

Note :

When a positive integer is divided by 2 the remainder is either 0 or 1. So, any positive integer will of the form 2k, 2k+1 for some integer k.

We may prove this in two cases.

Case 1 :

If x = even number  =  2k

product of two numbers  =  x (x + 1)

  =  2k(2k + 1)

Since the whole number is a multiple of 2, it is divisible by 2.

Case 2 :

If x = odd number  =  2k + 1

product of two numbers  =  x (x + 1)

  =  (2k + 1)(2k + 1 + 1)

=  (2k + 1)(2k + 2)

=  2 (k + 1)(2k + 1)

So, the product is divisible by 2.

So, the product of two consecutive number is divisible by 2.

Problem 4 :

When the positive integers a, b and c are divided by 13, the respective remainders are 9,7 and 10. Show that a+b+c is divisible by 13.

Solution :

divided = divisor x quotient + remainder

a  =  13 q₁ + 9  ----(1)

b  =  13 q₂ + 7----(2)

c  =  13 q₃ + 10----(3)

(1) + (2) + (3)

 a + b + c  =  13q₁ + 9 + 13q₂ + 7 + 13q₃ + 10

 a + b + c  =  13q₁ + 13q₂ + 13q₃ + 26

 a + b + c  =  13(q₁ + q₂ + q₃) + 13(2)

 a + b + c  =  13[(q₁ + q₂ + q₃) + 2]

So, a + b + c is divisible by 13.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.