PROBABILITY WORD PROBLEMS

Problem 1 :

Some boys are playing a game, in which the stone thrown by them landing in a circular region (given in the figure) is considered as win and landing other than the circular region is considered as loss. What is the probability to win the game?

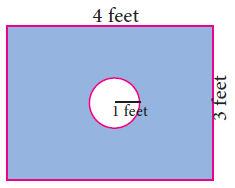
Solution :

Area of the rectangle  =  length x width

  =  3(4)

n(S)  =  12 square feet 

Area of circle  =  πr²

=  π(1)²

=  π

Probability of wining the game  =  π/12 

Problem 2 :

Two customers Priya and Amuthan are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another day. What is the probability that both will visit the shop on (i) the same day (ii) different days (iii) consecutive days?

Solution :

Sample space   

{(Mon, Mon), (Mon, Tues) (Mon, Wed) .... (Mon, Sat)

(Tues, Mon), (Tues, Tues) (Tues, Wed) .... (Tues, Sat)

....(Sat, Mon), (Sat, Tues) (Sat, Wed) .... (Sat, Sat)}

(i)  Let "A" be the event that both will visit the shop on the same day 

Total number of days that they will visit on the same day =6

A = { (Mon, Mon), (Tues, Tues), (Wed, Wed), (Thurs, Thurs), (Fri, Fri), (Sat, Sat) }

P(A) = 6/36 = 1/6

(ii)  Total number of days that can be consecutive =5

Let "B" be the event that both will visit the shop on different days 

Total number of different days = Total days - Total same day

Total number of different days = 36 - 6 = 30

P(B)  =  30/36  =  5/6

(iii)  Let "C" be the event that both will visit the shop on consecutive days 

C  =  {(Mon, Tues), (Tues, Wed), (Wed, Thurs), (Thurs, Fri), (Fri, Sat)}

P(C)  =  5/36

Problem 3 :

In a game, the entry fee is ₹150. Th e game consists of tossing a coin 3 times. Dhana bought a ticket for entry . If one or two heads show, she gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise she will lose. Find the probability that she (i) gets double entry fee (ii) just gets her entry fee (iii) loses the entry fee.

Solution :

Sample space  = {HHH. HHT, HTH, HTT, THH, THT, TTH, TTT}

n(S)  =  8

(i)  Let "A" be the event of getting double entry fee

In order to get double entry fee, she has to show 3 heads.

A  = {HHH}

n(A)  =  1

P(A)  =  n(A)/n(S)

 P(A)  =  1/8 

(ii) just gets her entry fee

Let "B" be the even of getting her entry fee.

In order to get entry fee, we have to show one or two heads.

B  =  {HHT, HTH, HTT, THH, THT, TTH}

n(B)  =  6

P(B)  =  n(B)/n(S)

P(B)  =  6/8

P(B)  =  3/4

(iii) loses the entry fee.

Let "C" be the event of loses the entry fee.

C  =  {TTT}

n(C)  =  1 

P(C)  =  n(C)/n(S)

P(C)  =  1/8

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.