WORD PROBLEMS INVOLVING OPERATIONS OF WHOLE NUMBERS

Problem 1 :

What number must be increased by 293 to get 648?

Solution :

Let x be the required number.

What must be increased by 293 to get 648

x + 293 = 648

x = 648 - 293

x = 355

Problem 2 :

A woman has $255 in her purse. She gives $35 to each of her five children. How much money does she have left?

Solution :

Amount she has in her purse = $255

Each child gets = $35

Amount distributed :

= 5($35)

= $175

Amount she has left :

= $255 - $175

= $80

Problem 3 :

The Year 8 students at a school are split into 4 equal classes of 27 students each. The school decides to increase the number of classes to 6. How many students will there be in each of the new classes, if the students are divided equally between them?

Solution :

Number of existing classes = 4

Number of students in total :

= 27(4)

= 108

Number of classes increased = 6

Number of students in each class :

= ¹⁰⁸⁄₆

= 18

Problem 4 :

My bank account contains $3621 and I make monthly withdrawals of $78 for 12 months. What is my new bank balance.

Solution :

My old balance = $3621

I make withfrawals $78 each month for 12 months.

Amount of withdrawal :

= 12($78)

= $936

My new balance :

= old balance - withdrawal

= $3621 - $936

= $2685

Problem 5 :

A contractor bought 34 loads of soil, each weighing 12 tonnes. If the soil cost $23 per tonne, what was the total cost ?

Solution :

Number of loads = 34

Weight of 1 load = 12 tonnes

Cost of soil = $23 per tonne

Number of tonnes :

= 34(12)

= 408 tonnes

Required cost :

= 408($23)

=  $9384

Problem 6 :

4 less than three times of a whole number is equal to 8. Find the whole number. 

Solution :

Let x be the required whole number.

From the given information,

3x - 4 = 8

Add 4 to both sides.

3x = 12

Divide both sides by 3.

x = 4

The whole number is 4.

Problem 7 :

The sum of two whole numbers is 8 and that of the difference is 2. Find the two whole numbers.

Solution :

Let x and y be the two required whole numbers such that x > y.

From the given information,

x + y = 8 ----(1)

x - y = 2 ----(2)

Add (1) and (2) :

2x = 10

Divide both sides by 2.

x = 5

Substitute x = 5 into (1).

5 + y = 8

Subtract 5 from both sides.

y = 3

The two whole numbers are 5 and 3.

Problem 8 :

In a two-digit whole number, the digit at the tens place is twice the digit at the ones place. If 18 is subtracted from it, the digits are reversed. Find the two-digit whole number.

Solution :

Let x be the digit in ones place.

Then the two-digit number is (2x)(x).

From the given information,

(2x)(x) - 18 = (x)(2x)

(10 ⋅ 2x) + (1 ⋅ x) - 18 = (10 ⋅ x) + (1 ⋅ 2x)

20x + x - 18 = 10x + 2x

21x - 18 = 12x

Subtract 12x from both sides.

9x - 18 = 0

Add 18 to both sides.

9x = 18

x = 2

The digit at the ones place is 2 and the digit at the tens place is 4.

So, the required two-digit number is 42.

Problem 9 :

A whole number consisting of two digits is four times the sum of its digits and if 27 be added to it, the digits are reversed. Find the whole number.

Solution :

Let xy be the required two-digit whole number.

Given : The two-digit whole is equal four times the sum of its digits

xy = 4(x + y)

(10 ⋅ x) + (1 ⋅ y) = 4x + 4y

10x + y = 4x + 4y

6x - 3y = 0

2x - y = 0

y = 2x ----(1)

Given : If 27 be added to it, the digits are reversed.

xy + 27 = yx

(10 ⋅ x) + (1 ⋅ y) + 27 = (10 ⋅ y) + (1 ⋅ x)

10x + y + 27 = 10y + x

9x - 9y + 27 = 0

x - y + 3 = 0

Substitute y = 2x.

x - 2x + 3 = 0

-x + 3 = 0

-x = -3

x = 3

Substitute x = 1 into (1).

y = 2(3)

y = 6

Therefore, the required two-digit whole number is 36.

Problem 10 :

What are the smallest and largest three-digit whole numbers which are evenly divisible by 7?

Solution :

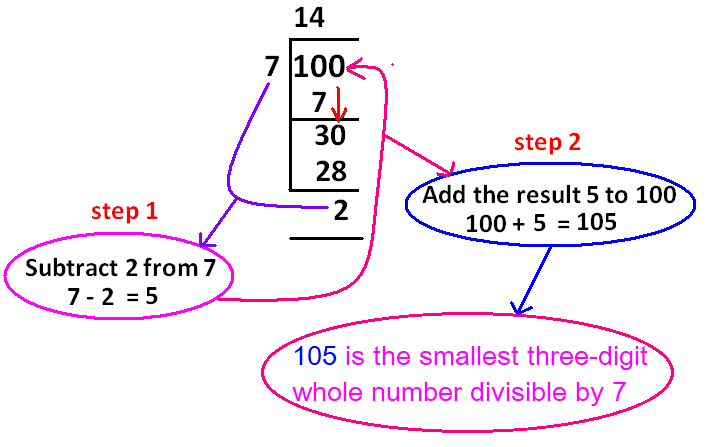
Steps to find the smallest three-digit whole number divisible by 7 :

Step 1 :

The smallest three-digit whole number is 100. Divide 100 by 7 and get the quotient and remainder.

When 100 is divided by 7, the quotient is 14 and the remainder is 2.

Step 2 :

Subtract the remainder 2 from the divisor 7.

= 7 - 2

= 5

Step 3 :

Add 5 to the dividend 100.

= 100 + 5

= 105

105 is the smallest three-digit number divisible by 7.

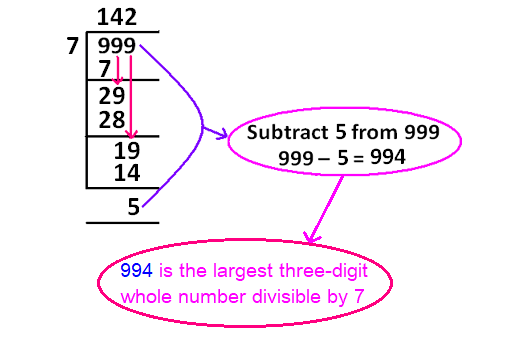
Steps to find the largest three-digit whole number divisible by 7 :

Step 1 :

The largest three-digit whole number is 999. Divide 999 by 7 and get the quotient and remainder.

When 999 is divided by 7, the quotient is 142 and the remainder is 5.

Step 2 :

Subtract the remainder 5 from the dividend 999.

= 999 - 5

= 994

994 is the largest three-digit number divisible by 7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.