WORD PROBLEMS INVOLVING PARABOLA AND HYPERBOLA

Problem 1 :

An engineer designs a satellite dish with a parabolic cross section. The dish is 5 m wide at the opening, and the focus is placed 1 2 . m from the vertex

(a) Position a coordinate system with the origin at the vertex and the x -axis on the parabola’s axis of symmetry and find an equation of the parabola.

(b) Find the depth of the satellite dish at the vertex.

Solution :

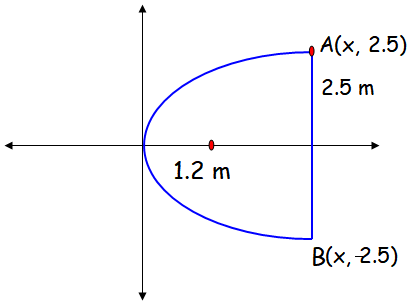
From the given information, the parabola is symmetric about x axis and open rightward.

y²  =  4ax

here a = 1.2

y²  =  4(1.2)x

y²  =  4.8 x

The parabola is passing through the point (x, 2.5)

(2.5)²  =  4.8 x

x  =  6.25/4.8

x  =  1.3 m

Hence the depth of the satellite dish is 1.3 m.

Problem 2 :

Parabolic cable of a 60 m portion of the roadbed of a suspension bridge are positioned as shown below. Vertical Cables are to be spaced every 6 m along this portion of the roadbed. Calculate the lengths of first two of these vertical cables from the vertex.

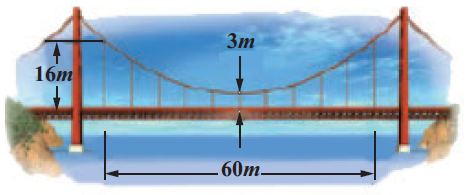
Solution :

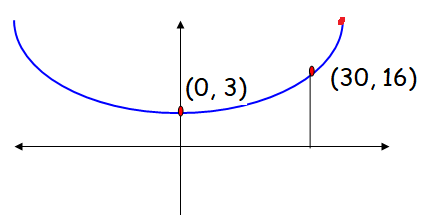
(x - h)²  =  4a(y - k)

(x - 0)²  =  4a(y - 3)

x²  =  4a(y - 3)

The parabola is passing through the point (30, 16)

30²  =  4a(16 - 3)

900  =  4a(13)

a  =  900/42

a  =  225/13

x²  =  4(225/13)(y - 3)

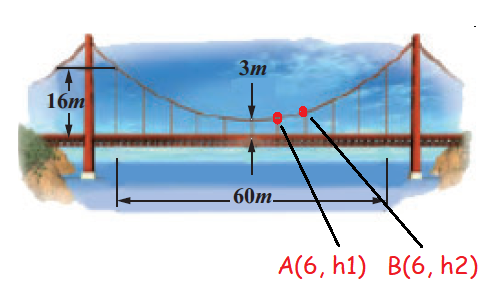
length of 1st cable :

6²  =  4(225/13)(h₁ - 3)

36(13)/4(225)  =  (h₁ - 3)

0.52 + 3  =  h₁

h₁  =  3.52 m

length of 2nd cable :

12²  =  4(225/13)(h₂ - 3)

144(13)/4(225)  =  (h₂ - 3)

2.08 + 3  =  h₂

h₂  =  5.08 m

Problem 3 :

Cross section of a Nuclear cooling tower is in the shape of a hyperbola with equation (x²/30²) - (y²/44²) = 1 . The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Find the diameter of the top and base of the tower.

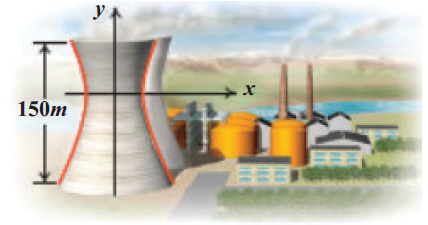
Solution :

Since the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola, let us consider 3y  =  150

 y  =  50

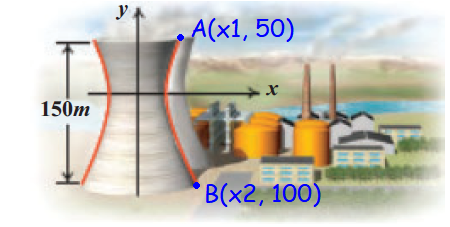
(x²/30²) - (y²/44²) = 1

By applying the point A in the general equation, we get

(x₁²/30²) - (50²/44²) = 1

(x₁²/30²)  =  1 +  (50²/44²) 

(x₁²/30²)  =  (1936 + 2500)/1936

(x₁²/30²)  =  4436/1936

x1²  =  (4436) (900)/1936

x₁  =  45.41

By applying the point B in the equation, we get

(x₂²/30²) - (100²/44²) = 1

(x₂²/30²)  =  1 +  (100²/44²) 

(x₂²/30²)  =  (1936 + 10000)/1936

(x₂²/30²)  =  11936/1936

x₂²  =  (11936) (900)/1936

x₂  =  74.45 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.