WORD PROBLEMS INVOLVING SIMILAR TRIANGLES WORKSHEET

Problem 1 :

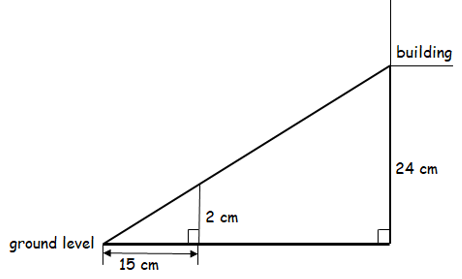
A ramp is built enable wheel-chair access to a building that is 24 cm above ground level. The ramp has a constant slope of 2 in 15, which means that for every 15 cm horizontally its rises 2 cm. Calculate the length of the base of the ramp.

Solution

Problem 2 :

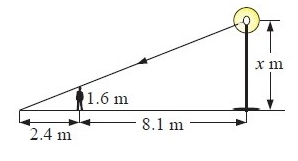
A boy who is 1.6 m tall casts a 2.4 m shadow when he stands 8.1 m from the base of an electric light pole. How high above the ground is the light globe ?

Solution

Problem 3 :

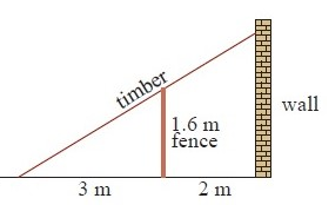
A piece of timber leaning against a wall, just touches the top of a fence, as shown. Find how far up the wall the timber reaches.

Solution

Problem 4 :

At the same time as the shadow cast by a vertical 30 cm long ruler is 45 cm long, Rafael’s shadow is 264 cm long.

a) Draw a fully labelled sketch of the situation.

b) Find Rafael’s height ?

Solution

Problem 5 :

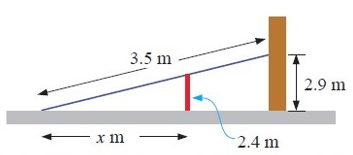
A 3.5 m ladder leans on a 2.4 m high fence. One end is on the ground and the other end touches a vertical wall 2.9 m from the ground. How far is the bottom of the ladder from the fence ?

Solution

Problem 6 :

Two surveyors estimate the height of a nearby mill. One stands 5 m away from the other on horizontal ground holding a 3 m stick vertically. The other surveyor finds a “line of sight” to the top of the hill, and observes this line passes the vertical stick at 2.4 m. They measures the distance from the stick to the top of the hill to be 1500 m using laser equipment. How high, correct to the nearest meter, is their estimate of the height of the hill ?

Solution

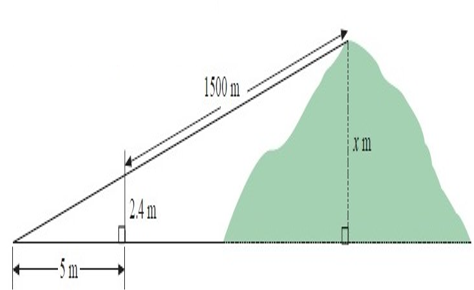
Problem 7 :

Find the width of the canyon.

Solution

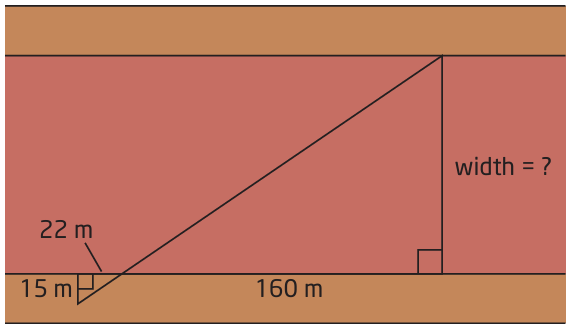
Problem 8 :

Use the dimensions of the surveyors’ triangles to find the width of the river, to the nearest metre.

Solution

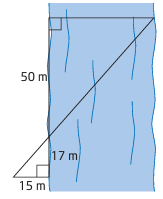
Example 9 :

In a diagram triangles ABC and EFG, AB = 12, EF = 30, BC = x and FG = 2x + 11. What is the value of x ?

Solution

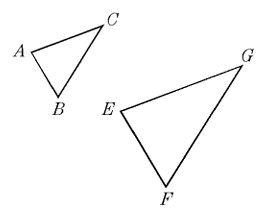
Example 10 :

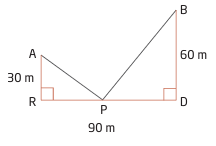
Two neighboring houses are located at A and B, near a straight section of a rural road, RD. The electric company plans to place a pole, P, at the roadside and connect wires from the pole to the two houses. How far from point R should the pole be located so that the minimum length of wire is needed?

Solution

Problem 1 :

Solution

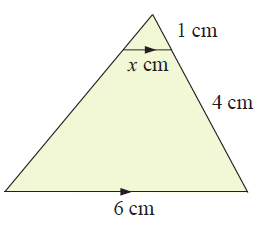
Problem 2 :

Solution

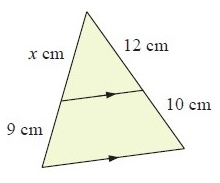
Problem 3 :

Solution

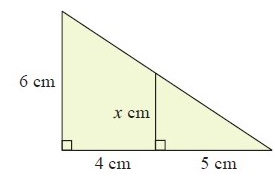
Problem 4 :

Solution

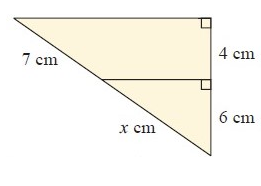
Problem 5 :

Solution

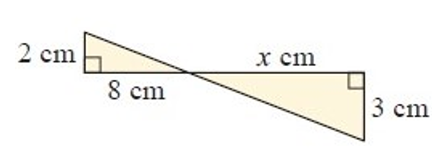
Problem 6 :

Solution

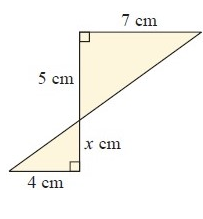
Problem 7 :

Solution

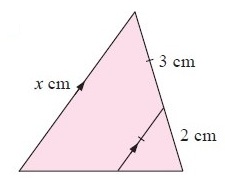
Problem 8 :

Solution

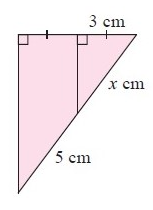
Problem 9 :

Solution

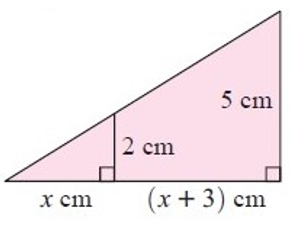
Problem 10 :

a) Find the missing angle in each triangle. How does this show that the triangles are similar?

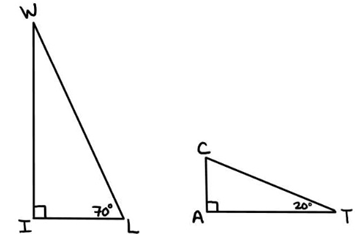
b) If 𝑾𝑰 = 𝟗.𝟒 and 𝑾𝑳 = 𝟏𝟎. Find the side 𝑰𝑳 using the Pythagorean Theorem (to one decimal)

c) If the scale factor from 𝚫𝑾𝑰𝑳 to 𝚫𝑻𝑨𝑪 is ½, find all the missing sides of triangle 𝚫𝑻𝑨𝑪.

Solution

Problem 11 :

On a sunny day Josée’s shadow is 2.9 m long, while the shadow of a tower is 11.3 m long. If Josée is 1.8 m tall, calculate the height of the tower.

Solution

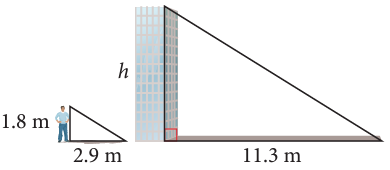
Problem 12 :

To measure the height of a tree, Cynthia has her little brother, BR, stand so that the tip of his shadow coincides with the tip of the tree’s shadow, at point C

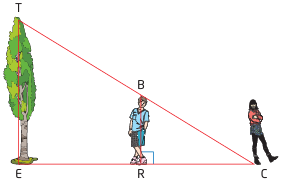
Cynthia’s brother, who is 1.2 m tall, is 4.2 m from Cynthia, who is standing at C, and 6.5 m from the base of the tree. Find the height of the tree, TE.

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.