WORD PROBLEMS INVOLVING THREE SETS

Question 1 :

In a college, 60 students enrolled in chemistry,40 in physics, 30 in biology, 15 in chemistry and physics,10 in physics and biology, 5 in biology and chemistry. No one enrolled in all the three. Find how many are enrolled in at least one of the subjects.

Solution :

Let C, P and B represent the subjects Chemistry, Physics and Biology respectively.

Venn diagram related to the information given in the question :

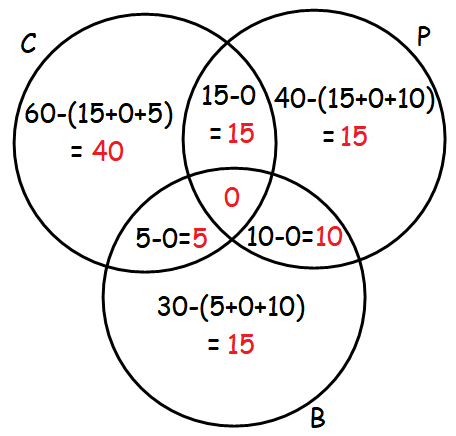
From the above Venn diagram, number of students enrolled in at least one of the subjects :

=  40 + 15 + 15 + 15 + 5 + 10 + 0

=  100

So, the number of students enrolled in at least one of the subjects is 100.

Question 2 :

In a town 85% of the people speak Tamil, 40% speak English and 20% speak Hindi. Also 32% speak English and Tamil, 13% speak Tamil and Hindi and 10% speak English and Hindi, find the percentage of people who can speak all the three languages.

Solution :

Let A, B and C are the people who speak Tamil, English and Hindi respectively.

Number of people who speak Tamil n (A)  =  85

Number of people who speak English n (B)  =  40

Number of people who speak Hindi n (C)  =  20

Number of people who speak English and Tamil

n (A∩B)  =  32

Number of people who speak Tamil and Hindi

n(A∩C)  =  13

Number of people who speak English and Hindi  

n(B∩C)  =  10

Let x be the number of people who speak all the three language.

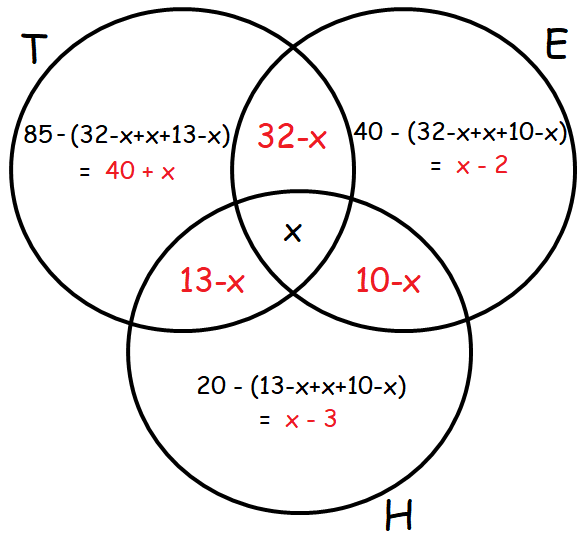
Total number of people =

100  =  40+x+32–x+x+13–x+10–x–2+x–3+x

100  =  40+32+13+10–2–3+x 

100  =  95–5+x

100  =  90+x 

x  =  100-90

x  =  10%

Question 3 :

An advertising agency finds that, of its 170 clients, 115 use Television, 110 use Radio and 130 use Magazines. Also 85 use Television and Magazines, 75 use Television and Radio, 95 use Radio and Magazines, 70 use all the three. Draw Venn diagram to represent these data. Find 

(i) how many use only Radio ?

(ii) how many use only Television ?

(iii) how many use Television and Magazine but not radio?

Solution :

Let A,B and C are the people who speak Television, Radio and Magazines respectively.

Number of people who use Television n(A)  =  115

Number of people who use Radio n(B)  =  110

Number of people who use Magazine n(C)  =  130

Number of people who use Television and Magazines

n(A∩C)  =  85

Number of people who use Television and Radio

n(A∩B)  =  75

Number of people who use Radio and Magazine

n(B∩C)  =  95

Number of people who use all the three n (A∩B∩C)  =  70

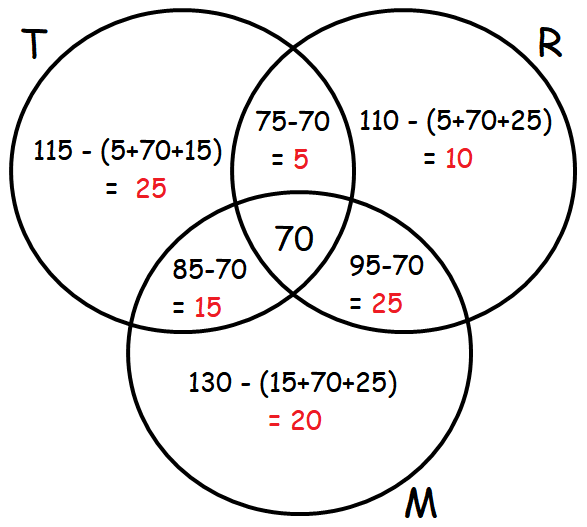
(i) Number of people who use only Radio  =  10

(ii) Number of people who use only Television  =  25

(iii) Number of people who use Television and Magazine but not radio  =  15

Related Pages

• Representation of Set 
  
• Types of set
• Disjoint sets 
• Power Set
  
• Operations on Sets
• Laws on set operations
• More Laws
• Venn diagrams
• Set word problems
• Relations and functions

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.