WORD PROBLEMS ON APPLICATION OF DERIVATIVES CALCULUS

Problem 1 :

A rectangular page is to contain 24 cm² of print. The margins at the top and bottom of the page are 1.5 cm and the margins at other sides of the page is 1 cm. What should be the dimensions of the page so that the area of the paper used is minimum.

Solution :

Given :

Area of the rectangle  =  24 cm²

Let x and y be the length and width of the rectangle respectively.

Horizontal measure  =  x

Including margin  =  x+2

Vertical measure  =  y

Including margin  =  y+3

xy  =  24

y  =  24/x

Area of the paper  =  (x+2) (y+3)

f(x)  =  (x+2)((24/x)+3)

f(x)  =  30 + 3x+48/x

f'(x)  =  3-48/x²

f'(x)  =  0

48/x²  =  3

x²  =  16

x  =  4, -4

f''(x)  =  0+96/x³

f''(x)  =  96/x³

f''(-4)  =  96/(-4)³ < 0 (Maximum)

f''(4)  =  96/(4)³ > 0 Minimum

When x  =  4, y = 24/4

y  =  6

Length including margin  =  4+2  ==> 6

Width including margin  =  6+3  ==> 9

Length and width of the rectangle is 6 cm and 9 cm.

Problem 2 :

A farmer plans to fence a rectangular pasture adjacent to a river. The pasture must contain 1,80,000 sq.mtrs in order to provide enough grass for herds. No fencing is needed along the river. What is the length of the minimum needed fencing material?

Solution :

Area  =  180000

Let x and y be the length and width of the rectangle.

xy  =  180000

y  =  180000/x

Perimeter of the fencing  =  2x + y

P(x)  =  2x+180000/x

p'(x)  =  2 - 180000/x²

p'(x)  =  0

180000/2  =  x²

90000  =  x²

x  =  300

p''(x)  =  -360000/x³

p''(300)  =  -360000/(300)³ < 0 (Maximum)

y  =  180000/300

y  =  600 m

Length of the material needed  =  2(300) + 600

=  600 + 600

=  1200 m

Problem 3 :

Find the dimensions of the rectangle with maximum area that can be inscribed in a circle of radius 10 cm.

Solution :

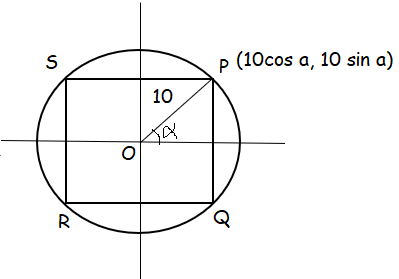
PQ  =  2(10 cos a)  ==>  20 cos a

SP  =  2(10 sin a)  ==>  20 sin a

Area of PQRS  =  (20 cos a) (20 sin a)

A(a)  =  200(sin 2a)

A'(a)  =  400 cos 2a

A'(a)  =  0

400 cos 2a  =  0

2a  =  cos^-1(0)

2a  =  π/2

a  =  π/4

A''(a)  =  -800 sin 2a

A''(a)  =  -800 sin 2(π/4)

A''(a)  =  -800 < 0 (Maximum)

PQ  =  20 cos π/4  =  20/√2  =  10√2

SP  =  20 sin π/4  =  20/√2  =  10√2

So, the dimensions are 10√2 cm, 10√2 cm.

Problem 4 :

Prove that among all the rectangles of the given perimeter, the square has the maximum area.

Solution :

Let x and y be the length and width of the rectangle.

Perimeter of the rectangle  P  =  2(x+y)

x+y  =  p/2

y  =  p/2 - x

Area of the rectangle f(x)  =  x y

=  x(p/2 - x)

=  xp/2 - x²

f'(x)  =  p/2 - 2x

f'(x)  =  0

p/2 - 2x  =  0

2x  =  p/2

x  =  p/4

f''(x)  =  0 - 2 < 0 (Maximum)

y  =  p/2 - x

Applying the value of x in the equation above, we get

y  =  p/2 - p/4

y  =  p/4

So, it is square.

Problem 5 :

The radius of a sphere is decreasing at a rate of 2 centimeters per second. At the instant when the radius of the sphere is 3 centimeters, what is the rate of change in square centimeters per second, of the surface area of the sphere ?

(The surface area S of a sphere with radius r is 4πr²)

Solution :

Surface area of sphere = 4πr²

Radius is decreasing at the rate of 2 cm per second, then dr/dt = -2 cm/s

radius = 3 cm

Differentiating with respect to x, we get

dS/dt = 4π(2r)(dr/dt)

= 8πr(dr/dt)

Applying r = 3 and dr/dt = -2 cm/s

dS/dt = 8π(3)(-2)

= -48π

So, surface area is decreasing at the rate of 48π cm²

Problem 6 :

The radius of a circle is increasing at a constant rate of 0.2 meters per second. What is the rate of increase in the area of the circle at the instance when the circumference is 20π meters ?

Solution :

Area of circle (A) = πr²

rate of change of radius(dr/dt) = 0.2 m/s

Perimeter of the circle =2πr

2πr = 20π

r = 10

dA/dt = 2πr (dr/dt)

= 2π(10) (0.2)

dA/dt = 4 π

So, the required increasing rate is 4 π.

Problem 7 :

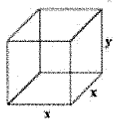
A box with a square base with no top has a surface area of 108 square feet. Find the dimension that will maximize the volume 

Solution :

Surface area of base with out top = 108 square feet

Since it is cube, all sides will be equal.

x² + 4xy = 108

4xy = 108 - x²

y = (108 - x²)/4x

Volume of cube = x² y 

x² (108 - x²)/4x

= x(108 - x²)/4

= (108x - x³)/4

V'(x) = (108 - 3x²) / 4

Finding critical number, V' (X) = 0

108 - 3x² = 0

3x² = 108

x² = 36

x = 6

Finding the second derivative :

V''(x) = - 6x/4

= - 3x/2

V''(6) =  - 3(6)/2

= -18/2

= -9 < 0 minimum

So, the required dimension of the cube is 6 feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.