WORD PROBLEMS ON ARITHMETIC SERIES

Problem 1 :

Find the sum of all odd positive integers less than 450.

Solution :

By wring the odd positive numbers less than 450, we get

1, 3, 5, 7, ...........447,449

1 + 3 + 5 + 7 +............. + 447 + 449

a = 1, d = 3 - 1  =  2, l =  449

S_n  =  (n/2)[a + l]

n = [(l - a)/d] + 1

n = [(449 - 1)/2] + 1

 =  (448/2) + 1

n  =  225

S_n  =  (225/2)[1 + 449]

=  (225/2) 450

S₂₂₅  =  50625

Problem 2 :

Find the sum of all natural numbers between 602 and 902 which are not divisible by 4.

Solution :

Sum of all natural number between 602 and 902

  =  Sum of all number between 602 and 902 - Sum of numbers which are divisible by 4 between 602 and 902

Sum of all number between 602 and 902 :

  =  [603 + 604 +................ + 901] 

Sum of numbers which are divisible by 4 between 602 and 902.

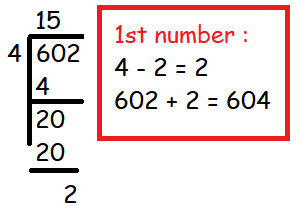
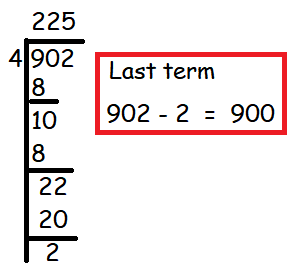
  =  604 + 608 + 612 + .......... + 900

n  =  [(l - a)/d] + 1

=  [(900 - 604)/4] + 1

n  =  75

S_n  =  (n/2)[a + l]

S₇₅  =  (75/2)[604 + 900]

  =  (75/2)[1504]

  =  75(752)

  =  56400

Required sum  =  224848 - 56400

=  168448

Problem 3 :

Raghu wish to buy a laptop. He can buy it by paying 40,000 cash or by giving it in 10 installments as 4800 in the first month, 4750 in the second month, 4700 in the third month and so on. If he pays the money in this fashion, find (i) total amount paid in 10 installments. (ii) how much extra amount that he has to pay than the cost?

Solution :

By writing the installments as series, we get

4800 + 4750 + 4700 +.............to 10 installments

Sn  =  (n/2)[2a + (n - 1) d]

n = 10, a = 4800, d = 4750 - 4800  =  -50

S_n  =  (n/2)[2a + (n - 1) d]

S₁₀  =  (10/2)[2(4800) + (10 - 1) (-50)]

  =  5[9600 + 9(-50)]

  =  5[9600 - 450]

  =  5[9150]

  =  45750

Extra amount paid by him  =  45750 - 40000

=  5750

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.