WORD PROBLEMS ON EQUATION OF PERPENDICULAR BISECTOR

A perpendicular bisector can be defined as a line segment which intersects another line perpendicularly and divides it into two equal parts. 

To find equation of perpendicular bisector which connects following points (x₁, y₁) and (x₂, y₂).

Example 1 :

Two post offices are located at P(3, 8) and Q(7, 2) on a council map. What is the equation of the line which should from the boundary between the two regions being serviced by the post offices ?

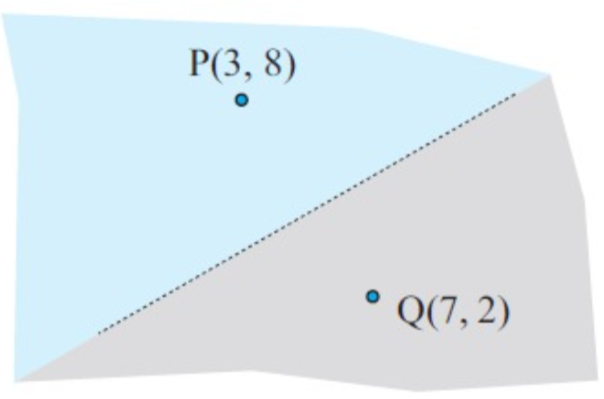
Solution :

Step 1 :

Midpoint of PQ  =  [(x₁ + x₂)/2, (y₁ + y₂)/2]

P(3, 8)------>(x₁, y₁)

Q(7, 2)------>(x₂, y₂)

Midpoint of PQ  =  [(3 + 7)/2, (8 + 2)/2]

=  [(10/2), (10/2)]

Midpoint of PQ  =  (5, 5)

Step 2 :

Slope of the line joining the points P and Q.

m  =  (y₂–y₁)/(x₂–x₁)

m  =  (2-8)/(7 – 3)

m  =  -6/4

m  =  -3/2

Step 3 :

Slope of perpendicular bisector  =  -1/(-3/2)

=  2/3

Step 4 :

Equation of perpendicular bisector :

y–y₁  =  m (x–x₁)

y-5  =  2/3 (x–5)

3y-15  =  2x–10

2x–3y+5  =  0

So, the equation of perpendicular bisector is

2x–3y+5  =  0

Example 2  :

Recall that the perpendicular bisector of a chord of a circle passes through The center of the circle. 

A circle passes through points P(5, 7), Q(7, 1) and R(- 1, 5). Find the Perpendicular bisectors of PQ and QR and solve them simultaneously to find The center of the circle.

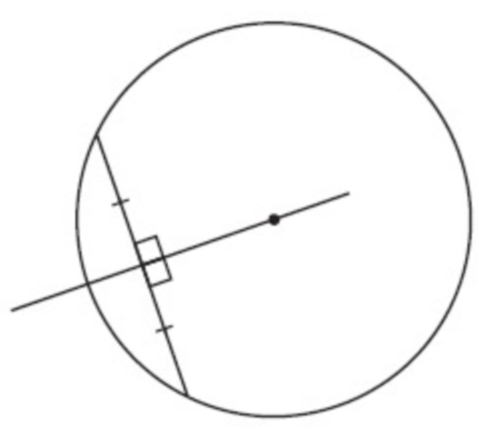
Solution :

P(5, 7), Q(7, 1) and R(- 1, 5)

First, we find the equation of the perpendicular bisector of PQ and QR.

Step 1 :

Midpoint of PQ  =  [(x₁+x₂)/2, (y₁+y₂)/2]

P(5, 7)------>(x₁, y₁)

Q(7, 1)------>(x₂, y₂)

Midpoint of PQ  =  [(5+7)/2, (7+1)/2]

Midpoint of PQ  =  (6, 4)

Step 2 :

Slope of PQ :

m  =  (y₂–y₁)/(x₂–x₁)

m  =  (1-7)/(7–5)

m  =  -6/2

m  =  -3

Step 3 :

Slope of perpendicular line  =  -1/(-3)  ==>  1/3

Equation of perpendicular bisector PQ :

y–y₁  =  m (x–x₁)

y-4  =  1/3 (x-6 )

3y-12  =  x–6

3y  =  x – 6 + 12

3y  =  x + 6

y  =  (1/3)x + 2-------(1)

Step 1 :

Midpoint of QR :

Q(7, 1)------>(x₁, y₁)

R(- 1, 5)------>(x₂, y₂)

Midpoint of QR  =  [(7-1)/2, (1+5)/2]

Midpoint of QR  =  (3, 3)

Step 2 :

Slope of QR :

m  =  (y₂ – y₁)/(x₂ – x₁)

m  =  (5 - 1)/(- 1 – 7)

m  =  - 4/8

m  =  - 1/2

Step 3 :

Slope of perpendicular(-1/m)  =  2

Step 4 :

y–y₁  =  m (x–x₁)

y-3  =  2 (x-3 )

y-3  =  2x–6

y  =  2x - 3

y  =  2x – 3 -------(2)

Now, To find the center of the circle,

By equating (1) and (2), we get

(1)  =  (2)

1/3x + 2  =  2x – 3

x + 6  =  6x – 9

x – 6x  =  - 9 – 6

- 5x  =  - 15

x  =  3

By applying x value in (2), we get

y  =  2x – 3

y  =  2(3) – 3

y  =  3

So, x  =  3 and y  =  3

Therefore, the center of the circle is (3, 3)

Example 3 :

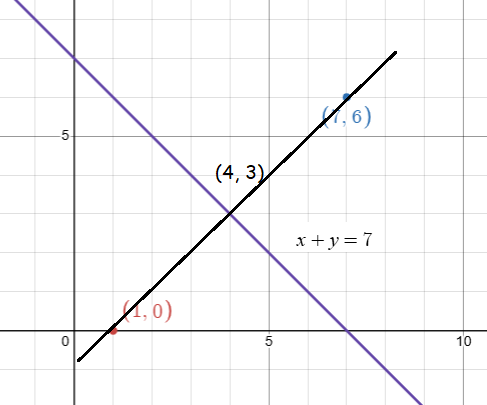
a. Graph points A(1, 0) and B(7, 6) and draw segment AB.

b) What point does the perpendicular bisector intersect segment AB?

c) What is the slope of the perpendicular bisector of segment AB?

d) What is the equation of the perpendicular bisector of segment AB?

e) Graph the perpendicular bisector on the graph.

Solution :

a) Plotting the points on the graph

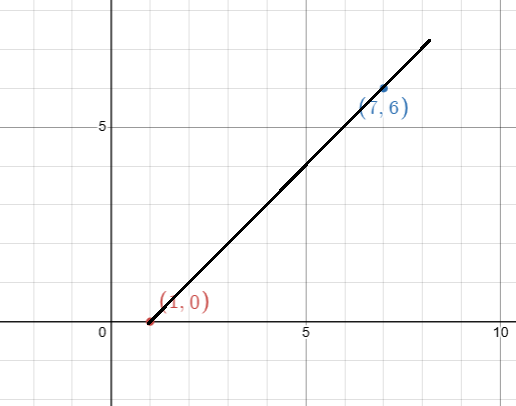
b)  The line joining the points A and B will intersect the perpendicular bisector exactly at the midpoint.

= (1 + 7)/2, (0 + 6)/2

= 8/2, 6/2

= (4, 3)

So, the perpendicular bisector will intersect the line AB at (4, 3).

c)  

To find the perpendicular bisector of the line joining the points A and B, we have to find the midpoint of the line and find the slope.

Midpoint of A and B:

A(1, 0) and B(7, 6)

m  =  (y₂ – y₁)/(x₂ – x₁)

=  (6 - 0)/(7 - 1)

= 6/6

= 1

Slope of perpendicular bisector = -1/m

= -1/1

= -1

d)  Equation of the perpendicular bisector :

y – y₁  =  m(x – x₁)

y - 3 = -1(x - 4)

y - 3 = -x + 4

x + y = 4 + 3

x + y = 7

So, the required equation of perpendicular bisector is x + y = 7

Example 4 :

If CD is a perpendicular bisector of AB.

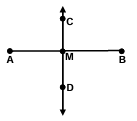
a) M is the midpoint of AB

b) M is the midpoint of CD.

c) Point C is equidistant from Points A and B.

d) If AC and BC were drawn ∆ABC would be isosceles.

e) Point D is equidistant from Points A and B

Solution :

Since CD is the perpendicular bisector of AB, M should the midpoint of the line AB.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.