WORD PROBLEMS ON INVERSE PROPORTION

Problem 1 :

6 pumps are required to fill a water sump in 1 hr 30 minutes. What will be the time taken to fill the sump if one pump is switched off ?

Solution :

Let x be the required time taken.

As the number of pumps increases the time taken to fill the sump will be less.

It comes under inverse proportion.

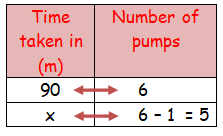
90 ⋅ 6 = x ⋅ 5

540 = x ⋅ 5

540/5 = x 

108 = x

108/60 = 1 hour 48 min

Therefore, the time taken to fill the sump is 1 hour 48 min.

Problem 2 :

A farmer has enough food for 144 ducks for 28 days. If he sells 32 ducks, how long will the food last? 

Solution :

Let the required number of days be x.

As the number of ducks decreases the food will last for more days.

It comes under inverse proportion.

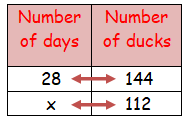
28 ⋅ 144 =  x ⋅ 112

4032 = x ⋅ 112

4032/112 = x

 36 = x

Therefore, the food last for 36 days.

Problem 3 :

If takes 60 days for 10 machines to dig a hole. Assuming that all machines work at the same speed, how long will it take 30 machines to dig the same hole?

Solution :

Let the number of days required be x.

As the number of machines increases it takes less days to complete the work.

It comes under inverse proportion.

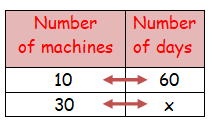
 10 ⋅ 60 = 30 ⋅ x

600 = 30 ⋅ x

600/30 = x

20 = x

Therefore, it takes 20 days to dig the hole.

Problem 4 :

Forty students stay in a hostel. They had food stock for 30 days. If the students are doubled then for how many days the stock will last?

Solution :

Let x be the required number of days.

As the number of students increases the food last for less number of days.

It comes under inverse proportion.

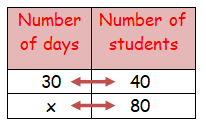
30 ⋅ 40 = x ⋅ 80

1200 = x ⋅ 80

1200/80 = x

15 = x

Therefore, the food stock lasts for 15 days.

Problem 5 :

Meena had enough money to send 8 parcels each weighing 500 grams through a courier service. What would be the weight of each parcel, if she has to send 40 parcels for the same money?

Solution :

Let the weight of parcel be x grams.

As the number of parcels increases weight of a parcel decreases.

It comes under inverse proportion.

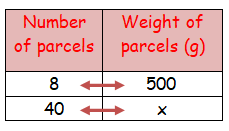
8 ⋅ 500 = 40 ⋅ x

4000 = 40 ⋅ x

4000/40 = x

100 = x

Therefore, the weight of each parcel is 100 grams.

Problem 6 :

If takes 120 minutes to weed a garden with 6 gardeners if the same work is to be done in 30 minutes, how many more gardeners are needed?

Solution :

Let the number of gardeners needed be x.

As the number of gardeners increases the time decreases.

It comes under inverse proportion.

6 ⋅ 120 = x ⋅ 30

720 = x ⋅ 30

720/30 = x

24 = x

To complete the work in 30 min gardeners needed = 24.

Already existing gardeners = 6

= 24 – 6

= 18

Therefore, 18 more gardeners are needed.

Problem 7 :

Heena goes by bi-cycle to her school every day. Her average speed is 12 km/hr. and she reaches school in 20 minutes. What is the increase in speed, if she reaches the school in 15 minutes?

Solution :

Let the speed to reach school in 15 minutes be x.

It comes under inverse proportion.

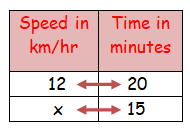
If she reaches the school in 15 minutes the speed = 16 km/hr.

Already running with 12 km/hr.

Increased speed = 16 – 12 = 4 km/hr.

Therefore, the increase in speed is 4 km/hr.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.