WORD PROBLEMS ON MENSURATION FOR GRADE 10

Problem 1 :

An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion be 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.

Solution :

Area of sheet required to make the funnel

  =  Curved surface area of frustum cone + Curved surface area of cylinder 

  =  π(R + r)l + 2πrh 

=  π [(R + r)l + 2rh]  ----(1)

Total height of funnel  =  22

Height of cylinder + Height of frustum cone  =  22

10 + h  =  22

h  =  22 - 10

h  =  12

Height of frustum cone  =  12 cm

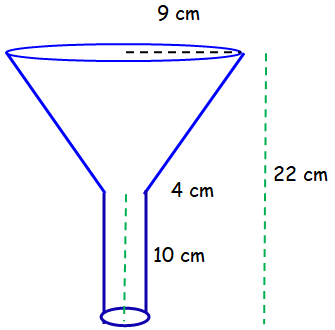
Radius of cylindrical portion (r) =  8/2  =  4 cm

Radius of the top of the frustum cone (R)  =  18/2  =  9 cm

l = √[h² + (R −r)²]

l = √[12² + (9 − 4)²]

l = √[12² + 5²]

l = √(144 + 25) = √169

l  =  13 cm

By applying these values in (1), we get

  =  π [(R + r)l + 2rh]  

  =  (22/7) [(9 + 4) (13) + 2 (4) (10)] 

  =  (22/7) [169 + 80] 

  =  782.57 cm²

Problem 2 :

Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.

Solution :

Radius of coin  (r₁)  =  (1.5/2) cm

height of coin (h₁) = thickness of coin 

=  2 mm  =  (2/10) cm

Radius of cylinder (r₂)  =  (4.5/2) cm

height of cylinder (h₂)  =  10 cm

n x Volume of 1 coin  =  Volume of cylinder

n x πr₁²h₁  =  πr₂²h₂

n  =  (4.5/2)² ⋅ 10 /  (1.5/2)² ⋅ (2/10)

=  450 coins

Problem 3 :

A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm and whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of solid cylinder.

Solution :

Volume of hollow cylinder  =  Volume of right circular cylinder

R =  4.3 cm, r = 1.1 cm, height = 4 cm

Height of right circular cylinder   =  12 cm

π h(R² - r²)  =  π r² h

4(4.3² - 1.1²)  =  r² (12)

r²  =   (4/12)(4.3 + 1.1) (4.3 - 1.1)

r²  =   (1/3) (5.4) (3.2)

r²  =   5.76

r = 2.4

Diameter of cylinder  =  2(2.4)  =  4.8 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.