WORD PROBLEMS ON PROBABILITY

Problem 1 :

In a box there are 20 non-defective and some defective bulbs. If the probability that a bulb selected at random from the box found to be defective is 3/8 then, find the number of defective bulbs.

Solution :

Number of non defective bulbs  =  20

Let "x" be the number of defective bulbs

Total number of bulbs n(S)  =  20 + x

Let "A" be the event of getting defective bulbs

P(A)  =  3/8  ---(1)

P(A)  =  x/(20 + x) ---(2)

(1)  =  (2)

3/8  =  x / (20 + x)

3(20 + x)  =  8x 

60 + 3x  =  8x

60  =  5x 

x  =  60/5  =  12

So, the number of defective bulbs is 12.

Problem 2 :

The king and queen of diamonds, queen and jack of hearts, jack and king of spades are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is (i) a clavor (ii) a queen of red card (iii) a king of black card

Solution :

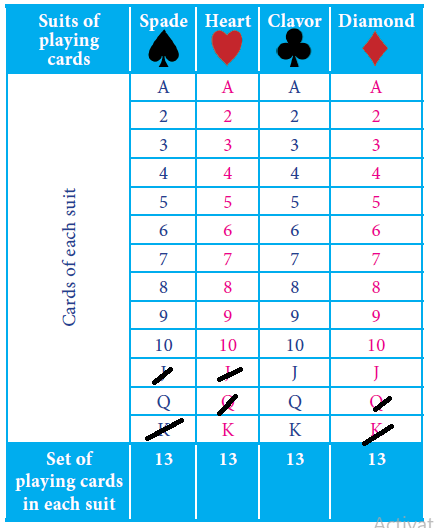
Total number of cards  =  52 - (1 + 1 + 1 + 1 + 1 + 1)

n(S)  =  52 - 6  =  46

(i) a clavor

Let "A" be the event of getting a clavor card. Since we donot remove any card from clavor, there must be 13 cards.

P(A)  =  n(A)/n(S)  

   P(A)  =  13/46

(ii) a queen of red card 

Let "B" be the event of getting queen of red card.

P(B)  = nP(B)/n(S)

We remove two queen cards from red.

P(B)  =  0

(iii) a king of black card

One black king will be in the deck.

n(D)  =  1

P(D)  =  n(D)/n(S)

P(D)  =  1/46

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.