WORD PROBLEMS ON SIMILARITY OF TRIANGLE

Problem 1 :

In the adjacent figure, triangle ABC is right angled at C and DE ⊥ AB . Prove that ΔABC ∼ ΔADE and hence find the lengths of AE and DE.

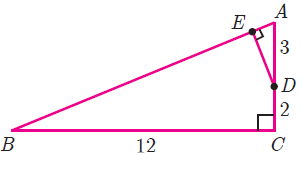
In triangle ABC,

AB²  =  BC² + AC²

AB²  =  12² + 5²

AB²  =  144 + 25  =  169

AB  =  13

In triangles ABC and EAD

<BCA  =  <AED

<CAB  =  <DAE

So, the triangles ABC and EAD are similar.

BC/EA  =  CA/ED  =  AB/AD

12/EA  =  (2+3)/ED  =  13/3

12/EA  =  5/ED  =  13/3

12/EA  =  13/3

EA  =  36/13

 5/ED  =  13/3

ED  =  5(3)/13

ED  =  15/13

Problem 2 :

In the adjacent figure, ΔACB  ∼ ΔAPQ . If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ.

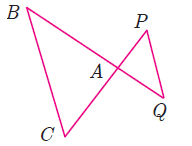
Solution :

Since the triangles ACB and APQ are similar.

BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm

BC/PQ (Angles opposite to <BAC and <PAQ)  --(1)

AC/PA (Angles opposite to <ABC and <AQP) --(2)

AB/AQ (Angles opposite to <ACB and <APQ) --(3)

(1)  =  (2)  =  (3)

BC/PQ  =  AC/PA  =  AB/AQ

8/4  =  AC/2.8  =  6.5/AQ

8/4  =  AC/2.8

AC  =  8(2.8)/4

AC  =  5.6 cm

8/4  =  6.5/AQ

AQ  =  6.5(4)/8

AQ  =  3.25 cm

Problem 3 :

If figure OPRQ is a square and <MLN = 90° . Prove that (i) ΔLOP ∼ ΔQMO (ii) ΔLOP ∼ ΔRPN (iii) ΔQMO ∼ ΔRPN (iv) QR² = MQ × RN

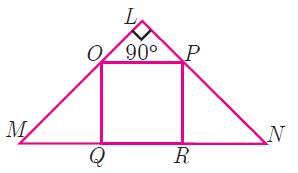
Solution :

(i) ΔLOP ∼ ΔQMO

In triangles ΔLOP  and ΔQMO

<OMQ  =  <LOP  (Corresponding angles)  A

<MQO  =  <OLP  (90)  A

OQ  =  OP  (side)

By ASA, the above triangles are similar. 

(ii) ΔLOP ∼ ΔRPN

<LPO  =  <PNR  (corresponding angles) A

<OLP  =  <PRN  (90) A

OP  =  PR (side)

By ASA, the above triangles are similar. 

(iii) ΔQMO ∼ ΔRPN 

<OQM  =  <PRN  (A)

OQ  =  PR  (Side)

Since the triangles ΔLOP and ΔQMO are similar,

OP/MO  =  OL/OQ  =  LP/MQ

OP/PN  =  OL/RN  =  LP/PR

MQ  =  PR  ----(1)

OQ  =  RN  ----(2)

MQ  =  RN

Hence the ΔQMO ∼ ΔRPN.

(iv) QR² = MQ × RN

Let us join OR,

OR²  =  OQ² + QR²

OP² + PR² -  OQ²  =  QR²

OP²  =  QR²

OP  =  MQ =  RN

OP (OP)  =   QR²

MQ x RN  =  QR²

Hence proved.

Problem 4 :

If ΔABC  ∼ ΔDEF such that area of ΔABC is 9cm² and the area of ΔDEF is 16cm² and BC = 2.1 cm. Find the length of EF.

Solution :

Since the ratio of area of two similar triangles is equal to the ratio of the squares of any two corresponding sides, we have

Area of ΔABC / Area of ΔDEF  =  BC²/EF²

(9/16)  =  (2.1)²/EF²

EF²  =  4.41 (16/9)

EF  =  2.8 cm

Problem 5 : 

Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y.

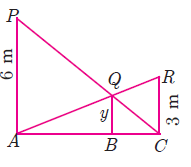
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.