WORD PROBLEMS TO FIND AREA OF QUADRILATERALS WITH VERTICES

How to Find Area of Quadrilateral with Coordinates

To find the area of the quadrilateral with the given four vertices, we may use the formula given below.

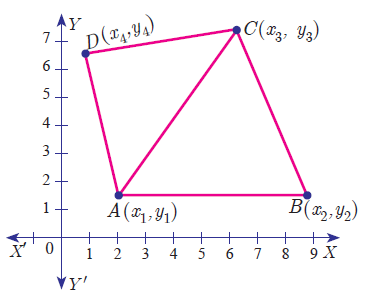
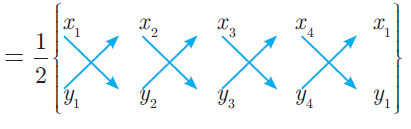
Question 1 :

Let P(11,7) , Q(13.5, 4) and R(9.5, 4) be the mid- points of the sides AB, BC and AC respectively of triangle ABC . Find the coordinates of the vertices A, B and C. Hence find the area of triangle ABC and compare this with area of triangle PQR

Solution :

To find the vertices of the triangle from the midpoint of the sides, please visit the page "https://www.onlinemath4all.com/how-to-find-the-vertices-of-a-triangle-if-the-midpoints-are-given.html"

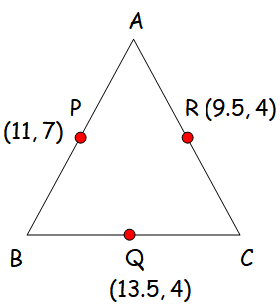
Vertex A :

  =  (11 + 9.5 - 13.5, 7 + 4 - 4)

  =  A (7, 7)

Vertex B :

  =  (11 + 13.5 - 9.5, 7 + 4 - 4)

  =  B (15, 7)

Vertex C :

  =  (13.5 + 9.5 - 11, 4 + 4 - 7)

  =  C (12, 1)

Area of triangle ABC :

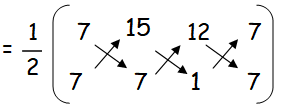
  =  (1/2)[(49 + 15 + 84) - (105 + 84 + 7)]

  =  (1/2)[148 - 196]

  =  48/2

Area of triangle ABC  =  24 square units

Area of triangle PQR :

P(11,7) , Q(13.5, 4) and R(9.5, 4) 

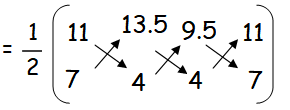
  =  (1/2)[(44 + 54 + 66.5) - (94.5 + 38 + 44)]

  =  (1/2)[164.5 - 176.5]

  =  (1/2) (12)

Area of triangle PQR  =  6

Area of triangle ABC  =  4 (Area of triangle PQR)

Let us look into the next example on "Word Problems to Find Area of Quadrilaterals with Vertices".

Question 2 :

In the figure, the quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio.

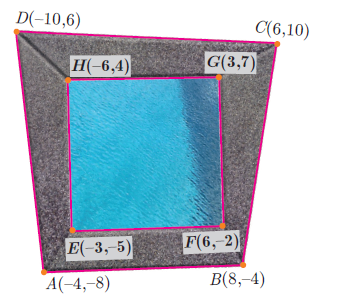
Solution :

To find the area of patio, we have to subtract area of EFGH from area of ABCD.

Area of ABCD :

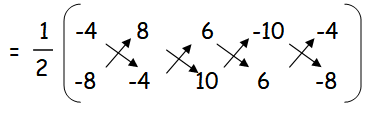
  =  (1/2)[(16 + 80 + 36 + 80) - (-64 - 24 - 100 - 24)]

  =  (1/2)[(212)-(-212)]

  =  (1/2)[212+212]

  =  212 square units

Area of EFGH :

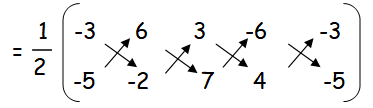
  =  (1/2)[(6 + 42 + 12 + 30) - (-30 - 6 - 42 - 12)]

  =  (1/2)[(90)-(-90)]

  =  (1/2)[90+90]

Area of EFGH  =  90 square units

Area of patio  =  212 - 90

  =  122 square units.

Question 3 :

A triangular shaped glass with vertices at A(-5,-4) , B(1,6) and C(7,-4) has to be painted. If one bucket of paint covers 6 square feets, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied.

Solution :

Area of triangle ABC  =  

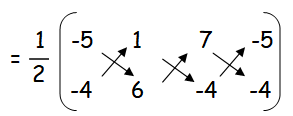
  =  (1/2)[(-30 - 4 - 28) - (-4 + 42 + 20)]

  =  (1/2)[-62 - (58)]

  =  (1/2)[-62 - 58]

  =  (1/2)(120)

  =  60 square feet

Area covered by one bucket of paint  =  6 square feets

Required number of bucket  =  60 / 6

  =  10 buckets

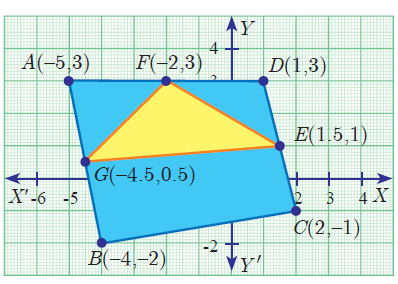
Question 4 :

In the figure, find the area of (i) triangle AGF (ii) triangle FED (iii) quadrilateral BCEG

Solution :

 (i) triangle AGF 

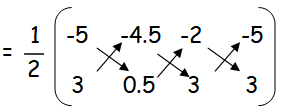
  =  (1/2) [(-2.5 - 13.5 - 6) - (-13.5 - 1 - 15)]

  =  (1/2) [(-22) - (-29.5)]

  =  (1/2) (-22+29.5)

  =  (1/2)[7.5]

  =  3.75 square units.

(ii) triangle FED

F (-2, 3) E (1.5, 1)  and D (1, 3)

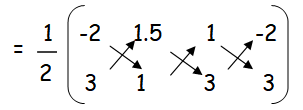
  =  (1/2)[(-2 + 4.5 + 3) - (4.5 + 1 - 6)]

  =  (1/2)[(5.5) - (-0.5)]

  =  (1/2)6

Area of triangle FED  =  3 square units.

(iii) B (-4, -2) C (2, -1) E (1.5, 1) G (-4.5, 0.5)

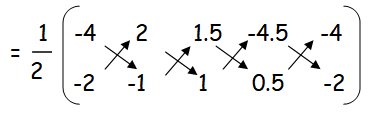
  =  (1/2)[(4 + 2 + 0.75 + 9) - (-4 - 1.5 - 4.5 - 2)]

  =  (1/2)[(15.75) - (-12)]

  =  (1/2)(15.75 + 12)

  =  (1/2)(27.75)

  =  13.875 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.