WORD PROBLEMS USING LAW OF SINES AND COSINES

Problem 1 :

A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the western most point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond.

Solution :

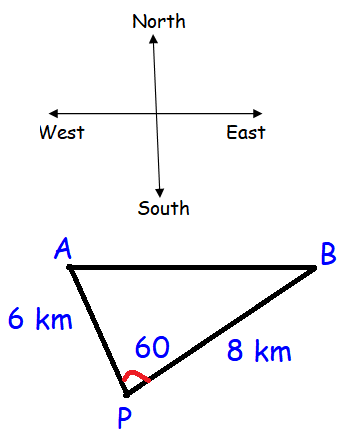
By finding the missing side, we may find the width of pond.

AP = a, PB = b and AB = c

cos C  =  (a² + b² - c²) / 2ab 

cos 60  =  (6² + 8² - c²) / 2(6)(8)

1/2  =  (36 + 64- c²) / 96

48  =  100 - c²

c²  =  100 - 48

c²  =  52

c  =  √52

=  2 √13 km

So, the width of pond is 2 √13 km.

Problem 2 :

Two Navy helicopters A and B are flying over the Bay of Bengal at same altitude from the sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10 km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends  60° at the boat, find the distance of the boat from B.

Solution :

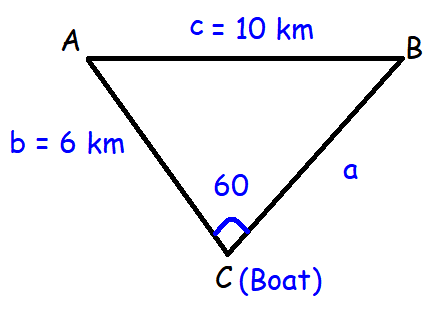
To find the missing side, we have to use the cosine formula. 

cos C  =  (a² + b² - c²)/2ab

Here we use the formula for cos C, because we know the length of b and c.

cos 60  =  (a² + 6² - 10²)/2(6)(10)

1/2  =  (a² -64)/2a(6)

1  =  a² - 64/6a

a² - 64  =  6a

a² - 6a - 64  =  0

 = (-b ± √b² - 4ac)/2a

=  (6 ± √(36 - 4(1)(-64))/2(1)

=  (6 ± √292)/2

=  (6 ± 2√73)/2

=  3 ± √73

So, the distance from the helicopter B to boat is 3 + √73 km.

Problem 3 :

A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3km, BP = 5 km and ∠APB = 120^◦, then find the length of the tunnel to be built

Solution :

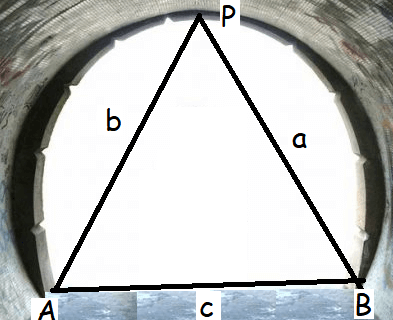
Given that :

AP = 3 km = b, BP = 5 km = a and ∠APB = 120^◦

cos C  =  (a² + b² - c²)/2ab

cos 120  =  (5² + 3² - c²)/2(5)(3)  

cos 120  =  cos (90+30)  =  sin 30  =  -1/2

-1/2  =  (25 + 9 - c²)/30

-15  =  34 - c²

c²   =  49, c = 7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.