WORKSHEET ON DISTANCE BETWEEN TWO POINTS

Problem 1 :

Find the distance between the two points given below. 

(-12, 3) and (2, 5)

Problem 2 :

Find the distance between the two points given below. 

(-2, -3) and (6, -5)

Problem 3 :

If the distance between the two points given below is 2√29, then find the value of k, given that k > 0.  

(-7, 2) and (3, k)

Problem 4 :

Find the distance between the points A and B in the xy-pane shown below. 

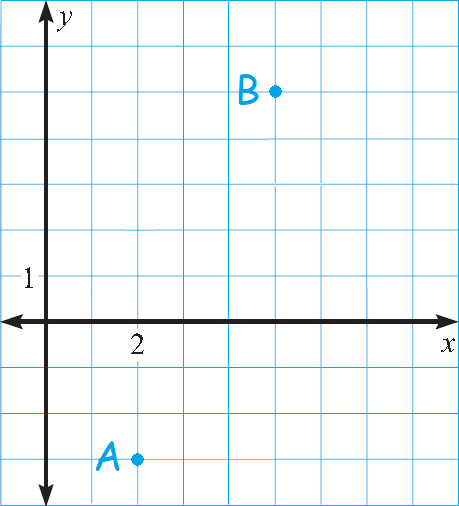
Problem 5 :

The figure shows a right triangle. Find the length of the hypotenuse to the nearest tenth.

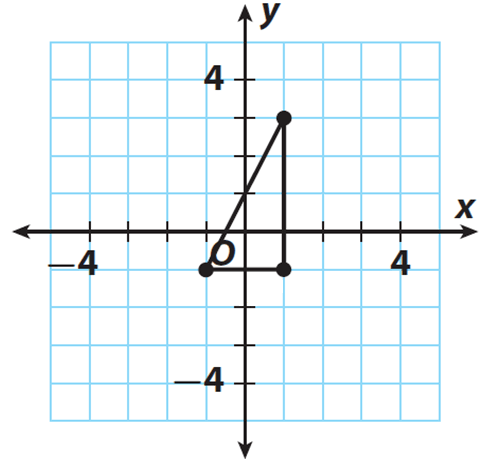
Problem 6 :

Gabriela wants to find the distance between her house on one side of a lake and the beach on the other side. She marks off a third point forming a right triangle, as shown in the figure. The distances in the diagram are measured in meters. Find the straight-line distance from Gabriela’s house to the beach using distance between two points formula. Check your answer using Pythagorean Theorem.

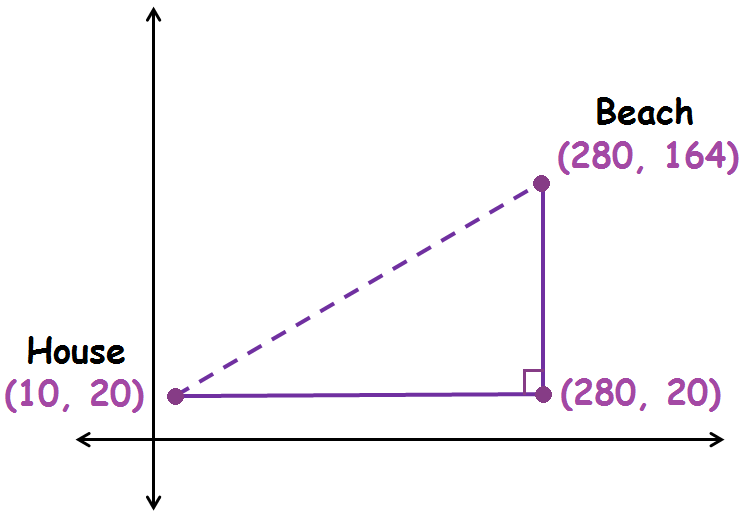
Answers

1. Answer :

(-12, 3) and (2, 5)

Formula for the distance between the two points is

√[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁)  =  (-12, 3) and (x₂, y₂)  =  (2, 5).

=  √[(2 + 12)² + (5 - 3)²]

=  √[14² + 2²]

=   √[196 + 4]

=  √200

=   √(2 ⋅ 10 ⋅ 10)

=   10√2

So, the distance between the given points is 10√2 units. 

2. Answer :

(-2, -3) and (6, -5)

Formula for the distance between the two points is

√[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁)  =  (-2, -3) and (x₂, y₂)  =  (6, -5).

=  √[(6 + 2)² + (-5 + 3)²]

=  √[8² + (-2)²]

=   √[64 + 4]

=  √68

=   √(2 ⋅ 2 ⋅ 17)

=   2√17

So, the distance between the given points is 2√17 units. 

3. Answer :

(-7, 2) and (3, k)

Distance between the above two points  =  2√29

√[(x₂ - x₁)² + (y₂ - y₁)²]  =  2√29

Substitute (x₁, y₁)  =  (-7, 2) and (x₂, y₂)  =  (3, k).

√[(3 + 7)² + (k - 2)²]  =  2√29

√[10² + (k - 2)²]  =  2√29

√[100 + (k - 2)²]  =  2√29

Square both sides. 

100 + (k - 2)²  =  (2√29)²

100 + k² - 2(k)(2) +  2²  =  2²(√29)²

100 + k² - 4k +  4  =  4(29)

k² - 4k + 104  =  116

Subtract 116 from each side.

k² - 4k - 12  =  0

(k - 6)(k + 2)  =  0

k - 6  =  0  or  k + 2  =  0

k  =  6  or  k  =  -2

Because k > 0, we have

k  =  6

4. Answer :

Identify the points A and B in the xy-plane above. 

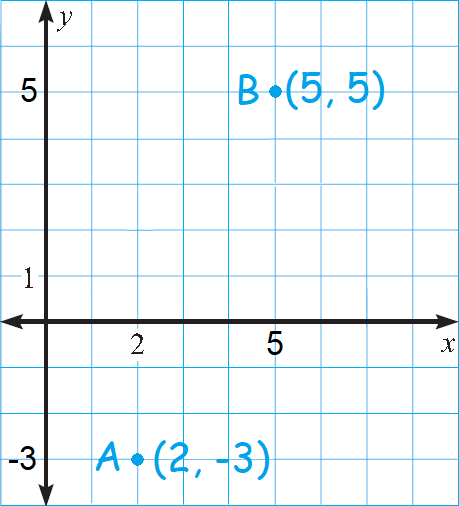
Formula for the distance between the two points is

√[(x₂ - x₁)² + (y₂ - y₁)²]

To find the distance between the points A and B, substitute (x₁, y₁)  =  (2, -3) and (x₂, y₂)  =  (5, 5).  

AB  =  √[(5 - 2)² + (5 + 3)²]

AB  =  √[3² + 8²]

AB  =  √(9 + 64)

AB  =  √73 units

5. Answer :

Mark the required coordinates to find the length of the hypotenuse.  

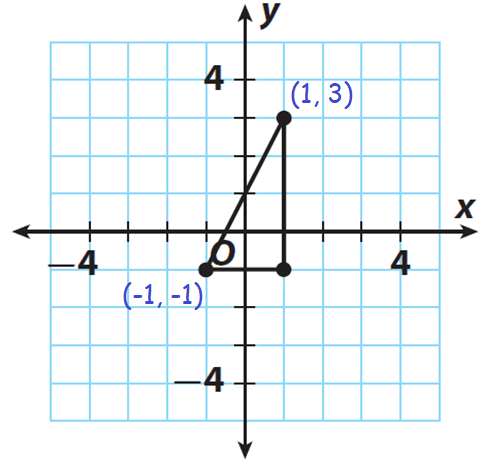
Length of the hypotenuse :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁)  =  (-1, -1) and (x₂, y₂)  =  (1, 3).  

=  √[(1 + 1)² + (3 + 1)²]

=  √[2² + 4²]

=  √(4 + 16)

=  √20

≈  4.5 units

6. Answer :

Straight-line distance from Gabriela’s house to the beach (using distance between two points formula) :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = (10, 20) and (x₂, y₂) = (280, 164).

=  √[(280 - 10)² + (164 - 20)²]

=  √[270² + 144²]

=  √(72900 + 20736)

=  √93636

= 306 meters

Checking the answer using Pythagorean Theorem :

Step 1 :

Find the length of the horizontal leg.

The length of the horizontal leg is the absolute value of the difference between the x-coordinates of the points (280, 20) and (10, 20).

|280 - 10|  =  270

The length of the horizontal leg is 270 meters.

Step 2 :

Find the length of the vertical leg.

The length of the vertical leg is the absolute value of the difference between the y-coordinates of the points (280, 164) and (280, 20).

|164 - 20|  =  144

The length of the vertical leg is 144 meters.

Step 3 :

Let a = 270, b = 144 and c represent the length of the hypotenuse. Use the Pythagorean Theorem to write the relationship between a, b and c.

a² + b²  =  c²

Step 4 :

Substitute a  =  270 and b  =  144 and solve for c. 

270² + 144²  =  c²

Simplify.

72,900 + 20,736  =  c²

93,636  =  c²

Take the square root of both sides.

√93,636  =  √c²

306  =  c

So, the distance from Jose’ house to the beach is 306 meters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.