WORKSHEET ON FINDING SLOPE FROM TWO POINTS

Find the slope of the line segment joining the following pairs of points

Find the missing coordinate given slope and two points

Problem 1 :

A(1, 3) to B(3, a) is parallel to a line with gradient 3.

Solution

Problem 2 :

P (a, -3) to Q(4, -2) is parallel to a line with gradient 1/3.

Solution

Problem 3 :

M(3, a) to N(a, 5) is parallel to a line with gradient -2/5.

Solution

Problem 4 :

A(2, -3) to B(-2, t) is perpendicular to a line with gradient 1 1/4.

Solution

Problem 5 :

C(t, -2) to D(1, 4) is perpendicular to a line with gradient 2/3.

Solution

Problem 6 :

P(t, -2) to Q(5, t) is perpendicular to a line with gradient -1/4.

Solution

Problem 7 :

Find the slope of the line that contains the points (3, 4) and (7, 13).

Solution

Problem 8 :

Find the slope of the line that contains the points (2, 11) and (6,−5).

Solution

Problem 9 :

Find a number t such that the line containing the points (1, t) and (3, 7) has slope 5.

Solution

Problem 10 :

Find a number c such that the line containing the points (c, 4) and (−2, 9) has slope −3.

Solution

Problem 11 :

Find a number t such that the point (3, t) is on the line containing the points (7, 6) and (14, 10).

Solution

Answers :

Find the slope of the line using formula.

Problem 1 :

Solution

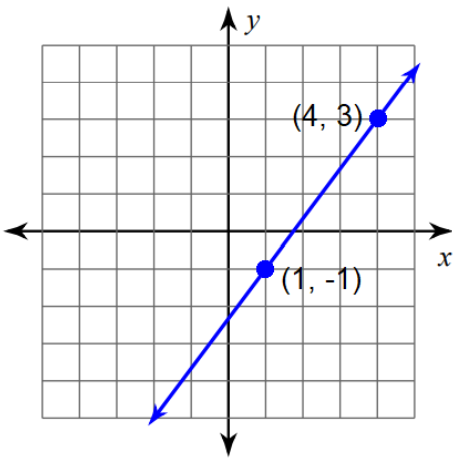
Problem 2 :

Solution

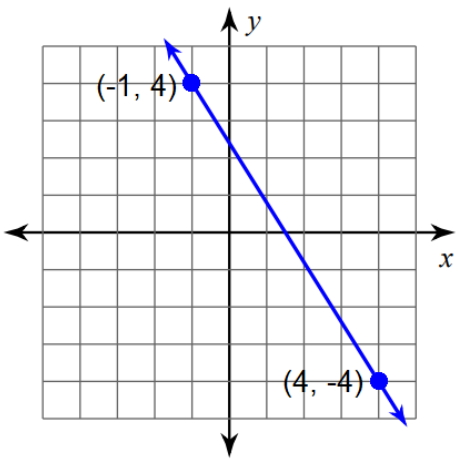
Problem 3 :

Solution

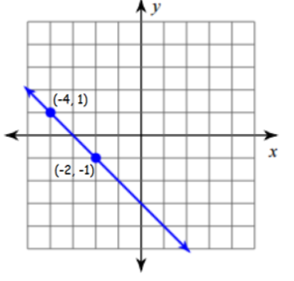
Answers :

1)  Slope  =  4/3

2)  Slope  =  -8/5

3)  Slope  =  -1

Problem 1 :

Suppose that a bike rents for $4 plus $1.50 per hour. Write an equation in slope-intercept form that models this situation.

Solution

Problem 2 :

In order to become a member of the library-all-star-members club, there is a $40 sign-up fee and a $2 monthly fee. Write an equation in slope-intercept form that models this situation. Use the equation to find the total cost of being an all-star library member for 19 months.

Solution

Problem 3 :

A taxi service charges a fixed rate of $30 and $3 per mile. Write an equation in slope-intercept form that models this situation. Use the equation to find the total cost for an 18-miles trip.

Solution

Problem 4 :

The U.S. Bureau of the Census predicted that the population of Florida would be about 17.4 million in 2010 and then would increase by about 0.22 million per year until 2015. Which of the following linear models predicts the population, y, of Florida (in millions) in terms of x, the number of years since 2010?

(A)  y = 17.4x + 0.22

(B)  y = -0.22x + 17.4

(C)  y = 0.22x + 17.4

(D)  y = -17.4x + 0.22

Solution

Problem 5 :

In 2005, 120 students at Lincoln High School had smart phones. By 2010, 345 students in the same school had smart phones. Write a linear model which predicts the number of students having smart phones and estimate the number of students having smart phones in 2018.

Solution

Problem 6 :

A cab service charges a fixed rate of $50 for a trip of 10 miles or less. It is charged $4 for each additional mile apart from 10 miles. Write an equation in slope-intercept form which gives the total cost for a trip of more than 10 miles. Use the equation to find the total cost of a 25-miles trip.

Solution

Answer Key

1)  y = 1.5x + 4

2) The total cost of being an all-star library member for 19 months is $78.

3)  The total cost for an 18-miles trip is $84.

4)  

y = 0.22x + 17.4

Therefore, the correct answer is option is option (C).

5)  It is estimated that there would be 480 students having smart phone in 2008.

6)  The total cost of a 25-miles trip is $110.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.