WORKSHEET ON PROPERTIES OF LOGARITHMS

Question 1 :

If a² + b² = 7ab, show that :

log(a+b)/3  =  1/2(log a+log b)

Question 2 :

Prove :

log(a²/bc) + log (b²/ac) + log (c²/ab)  =  0

Question 3 :

Prove :

log 2 + 16 log (16/15) + 12 log (25/24) + 7 log(81/80)  =  1

Question 4 :

Prove :  

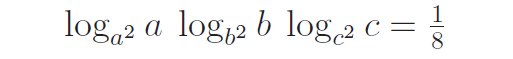
Question 5 :

Prove :

log a + log a² + log a³ + · · · + log aⁿ = (n(n+1)/2) log a

Question 6 :

If log x/(y - z)  =  log y/(z - x)  =  log z/(x - y), then prove : 

xyz  =  1

Question 7 :

Solve for x :

log₂x − 3log_1/2x  =  6

Question 8 :

Solve for x :

log_5-x(x² − 6x + 65)  =  2

Detailed Answer Key

Question 1 :

If a² + b² = 7ab, show that :

log(a+b)/3  =  1/2(log a+log b)

Answer :

Given that :

a² + b² = 7ab

Add 2ab on both sides 

a² + b² + 2ab = 7ab + 2ab

(a + b)²  =  9ab

(a + b)  =  √(9ab)  ==>  a + b  =  3√(ab)

(a + b)/3  =  (ab)^1/2

Take log on both sides

log (a + b)/3  =  log (ab)^1/2

log (a + b)/3  =  (1/2)(log a + log b)

Hence proved.

Question 2 :

Prove :

log(a²/bc) + log (b²/ac) + log (c²/ab)  =  0

Answer :

L.H.S  =  log (a²/bc) + log (b²/ac) + log (c²/ab)

L.H.S  =  log (a²/bc) ⋅ (b²/ac) ⋅ (c²/ab)

L.H.S  =  log 1

L.H.S  =  0

L.H.S  =  R.H.S

Hence proved.

Question 3 :

Prove :

log 2 + 16 log (16/15) + 12 log (25/24) + 7 log(81/80)  =  1

Answer :

L.H.S

log 2 + 16 log (16/15) + 12 log (25/24) + 7 log(81/80)  =  1

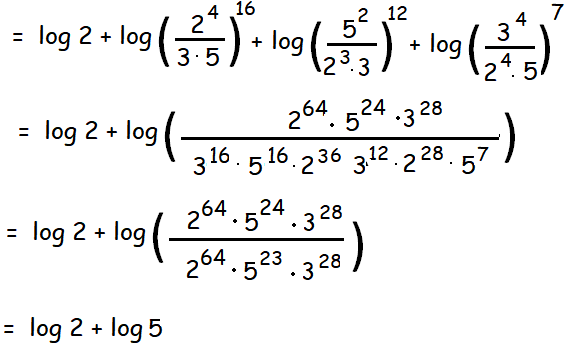
  =  log 10

  =   1  =  R.H.S

Hence proved

Question 4 :

Prove :  

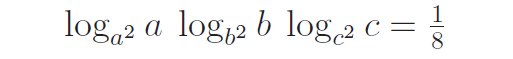
Answer :

L.H.S

Let us use base change rule,

  =  (1/log_a a²) ⋅ (1/log_b b²) ⋅ (1/log_c c²)

  =  (1/2log_aa) ⋅ (1/2log_bb) ⋅ (1/2log_cc)

  =  (1/2) ⋅ (1/2) ⋅ (1/2)

  =  1/8

Hence proved

Question 5 :

Prove :

log a + log a² + log a³ + · · · + log aⁿ = (n(n+1)/2) log a

Answer :

L.H.S  =  log a + log a² + log a³ + · · · + log aⁿ

L.H.S  =  1log a + 2log a + 3log a + · · · + nlog a

  L.H.S  =  log a (1 + 2 + 3 + · · · + n)

  L.H.S  =  log a (n(n + 1)/2)

  L.H.S  =  [n(n+1)/2] ⋅ log a

L.H.S  =  R.H.S

Hence proved.

Question 6 :

If log x/(y - z)  =  log y/(z - x)  =  log z/(x - y), then prove : 

xyz  =  1

Answer :

log x  =  k(y-z)  == > ky - kz   ------(1)

log y  =  k(z-x) == > kz - kx   ------(2)

log z  =  k(x-y) == > kx - ky   ------(3)

(1) + (2) + (3)

log x + log y + log z =  ky - kz + kz + kx + kx - ky

log x + log y + log z =  0

log (xyz)  =  0

xyz  =  1

Hence proved.

Question 7 :

Solve for x :

log₂x − 3log_1/2x  =  6

Answer : 

log₂ x − 3log _1/2 x  =  6

[1 / log_x 2]  −  [3 / log_x 1/2]  =  6

[1 / log_x 2]  −  [3 / (log_x 1 - log_x 2)]  =  6

[1 / log_x 2]  −  [3 / (0 - log_x 2)]  =  6

[1 / log_x 2]  −  [3 / (- log_x 2)]  =  6

[1 / log_x 2]  −  [- 3 / log_x 2]  =  6

[1 / log_x 2]  +  [3 / log_x 2]  =  6

(1 + 3) / log_x 2  =  6

4 / log_x 2  =  6

4log₂x  =  6

Divide both sides by 4. 

log₂x  =  6 / 4

log₂x  =  3 / 2

x  =  2^3/2

x  =  2√2

Hence, the value of x is 2√2.

Question 8 :

Solve for x :

log_5-x(x² − 6x + 65)  =  2

Answer : 

log_5-x (x² − 6x + 65)  =  2

x² − 6x + 65  =  (5 - x)²

x² − 6x + 65  =  5² - 2 ⋅ x ⋅ 5 + x²

x² − 6x + 65  =  25 - 10x + x²

Simplify.

4x  =  - 40

Divide both sides by 4.

x  =  - 10

Hence, the value of x is -10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.